Systematic absences are ‘missing’ diffraction intensities on a powder X-ray diffraction spectrum of intensity versus 2θ. Consider the possible values of h, k and l that satisfy Bragg’s equation of for a primitive cubic unit cell:
| hkl | 100 | 110 | 111 | 200 | 210 | 211 | 220 | 300 | 221 |
| h2 + k2 + l2 | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 9 |
9 |
7 is missing in the h2 + k2 + l2 sequence, as h, k and l are integers. An extension of the sequence reveals that 15, 23, etc. are missing as well. Hence, the spectrum for a primitive cubic unit cell has a specific set of missing intensities. Likewise, different missing intensity sets are expected for other unit cells. For example, a sample with grains that are composed of face-centred cubic unit cells (figure I below) has scattered rays from {200} planes that are out of phase with rays from {100} (figure II), resulting in destructive interference with no {100} intensity peak on the spectrum.
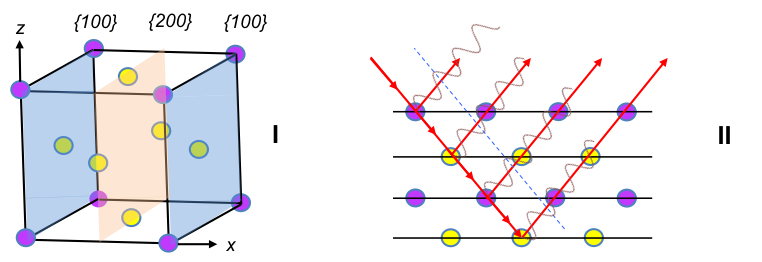
In fact, for all face-centred cubic unit cells (FCC), intensity peaks are observed when the integers h, k and l are either all odd or all even, e.g. {111}, {200}, {220}, …. A mathematical treatment of this requires the knowledge of the structure factor, which is described in a later section. The structure factor for a body-centred cubic unit cell (BCC) also shows that systematic absences do not appear when h + k + l = 2n, i.e. when the sum of the Miller indices is even, e.g. {110}, {200}, {211}, ….

Question
Identify the cubic unit cells of polonium and aluminium and determine their dimensions using the following powder X-ray diffraction spectral data:
| 2θi | 2θ1 | 2θ2 | 2θ3 | 2θ4 | 2θ5 | 2θ6 | 2θ7 | 2θ8 |
|
Po |
12.1o | 17.1o | 21.0o | 24.3o | 27.2o | 29.9o | 34.7o |
36.9o |
|
Al |
38.4 o | 44.7 o | 65.0 o | 78.1 o | 82.3 o | 98.9 o | 111.8 o | 116.4 o |
λAl = 71.0 pm and λPo = 154.1 pm
Answer
Let’s tabulate the systematic absences of the three cubic unit cells for reference, knowing that i) 7 is missing for a primitive cubic cell, ii) the integers h, k and l for an FCC cell are either all odd or all even, and iii) that h + k + l = 2n for a BCC cell.
| hkl | 100 | 110 | 111 | 200 | 210 | 211 | 220 | 300 |
221 |
|
| h2+ k2 + l2 |
Primitive |
1 | 2 | 3 | 4 | 5 | 6 | 8 | 9 |
9 |
|
BCC |
– | 2 | – | 4 | – | 6 | 8 | – |
– |
|
|
FCC |
– | – | 3 | 4 | – | – | 8 | – | – | |
Squaring both sides of eq13, we have
If the unit cell is primitive, the successive ratios of will produce the sequence 1,2,3,4,5,6,8,9… since from eq14,
and
. If the unit cell is BCC, we need to multiply the successive ratios of
by the factor 2 to obtain the fingerprint sequence of 2,4,6,8… since
. By the same logic, the multiplication factor is 3 if the unit cell is FCC. Tabulating the ratios,
|
|
||||||||
|
Po |
1.00 | 1.99 | 2.99 | 3.99 | 4.98 | 5.99 | 8.01 |
9.02 |
|
Al |
1.00 | 1.34 | 2.67 | 3.67 | 4.00 | 5.34 | 6.34 |
6.68 |
it is clear that the unit cell for polonium is primitive cubic while that for aluminium is FCC. To verify the fingerprint sequence of an FCC unit cell, we multiply the aluminium ratios by the factor of 3:
|
|
||||||||
|
Al x3 |
3.00 | 4.01 | 8.01 | 11.01 | 12.01 | 16.01 | 19.02 |
20.04 |
Finally, the dimensions of the unit cell of each sample is obtained by substituting any corresponding set of θ and hkl values in eq14:
|
|
a |
|
Po |
337 pm |
| Al |
406 pm |
As mentioned above, to mathematically show that the integers h, k and l for an FCC cell are either all odd or all even, and that h + k + l = 2n for a BCC cell, we need to explain what the structure factor is. To do this, we must first understand the Laue equations and the scattering factor.
