Term symbols (quantum mechanics)

Term symbols are notations representing energy levels of a particular electron configuration of a chemical species.

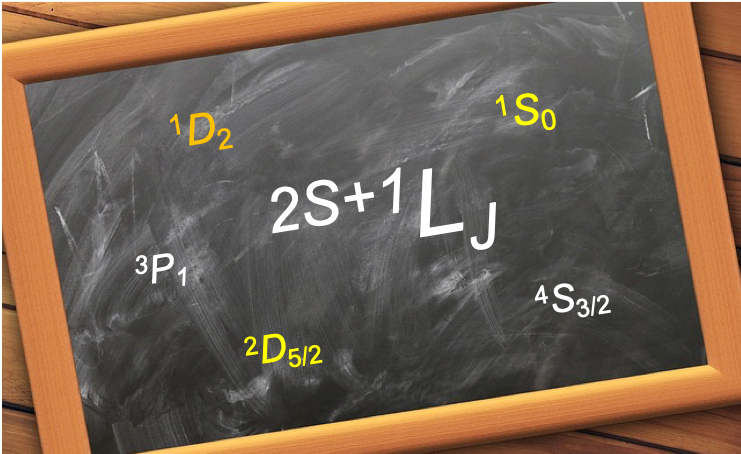
Atomic term symbols

For light atoms, an atomic term symbol is based on Russell Saunders (LS) coupling and can be expressed either as:

$^{2S+1}L\; \; \; \; \; \; \; \; 291$

$^{2S+1}L_J\; \; \; \; \; \; \; \; 292$

where $2S+1$ is called the multiplicity of the term symbol, $S$ is the total spin angular momentum quantum number, $L$ is the total orbital angular momentum quantum number and $J$ is the total angular momentum quantum number.

Each value of $L$ is further assigned a letter:

L	0	1	2	3	4	5	6	7	8
Letter	S	P	D	F	G	H	I	K	L

Energy levels denoted by eq291 ignore spin-orbit coupling and are called terms, while those denoted by eq292 take into account spin-orbit coupling and are known as levels. Eq291 implies that for a particular electron configuration of an atom, states with the same set of angular momentum quantum numbers $L$ and $S$ have the same energy. We have shown in an earlier article how this is possible. When spin-orbit coupling effects are considered, degenerate states corresponding to a term are split into multiple levels. From eq248 and eq289, energy levels of a particular electron configuration of an atom are dependent on the quantum numbers $J$ , $L$ and $S$ .

Question

Write the term symbols for i) the ground state of the hydrogen atom, and ii) the excited state of the hydrogen atom with the electron in the 2p orbital.

Answer

For the ground state of hydrogen, where $S=s=\frac{1}{2}$ and $L=0\equiv S$ , it is denoted by $^2S_{\frac{1}{2}}$ . For the excited state, the electron can be in any of the three degenerate 2p orbitals with either an up spin or a down spin. We would therefore expect two term symbols. The first symbol is $^2P_{\frac{3}{2}}$ , while the second symbol is obtained using the Clebsch-Gordan series of eq219 and is $^2P_{\frac{1}{2}}$ .

Question

Why is a term symbol not described by the principal quantum number $n$ ?

Answer

Term symbols focus on the variation of energy resulting from the arrangement and interaction of electrons in subshells. These arrangements, known as microstates, depend on whether the electrons are equivalent (belonging to the same subshell) or non-equivalent (belonging to different subshells). For example, the electrons in the configuration $2p^2$ are equivalent, while those in $2p^13p^1$ are not. The term symbols for $2p^2$ and $2p^13p^1$ are $^1S,^1D,^3P$ and $^3D,^1D,^3P,^1P,^3S,^1S$ respectively. Although the term symbols for $2p^2$ and $3p^2$ are the same, the energies of the terms for $2p^2$ , which are determined spectroscopically, differ from those for $3p^2$ . Therefore, while the energy associated with $n$ does influence the overall energy of the electron within the atom, it doesn’t directly contribute to the variation in energies of electrons within the subshells.

As we move down the periodic table to heavier elements, such as lead or the actinides, spin-orbit interactions become so strong that $L$ and $S$ are no longer good quantum numbers. In these cases, we switch to jj-coupling, where the individual $\boldsymbol{\mathit{L}}_i$ and $\boldsymbol{\mathit{S}}_i$ couple to form a $\boldsymbol{\mathit{J}}_i$ for each electron, and the total angular momentum of the atom is obtained by vectorially adding these: $\boldsymbol{\mathit{J}}=\sum_i\boldsymbol{\mathit{J}}_i$ . The corresponding atomic term symbol is:

$(J_1,J_2,\cdots)_J$

For example, the term symbols for the $p^2$ configuration (see this article for details) are $\biggr$\frac{1}{2},\frac{1}{2}\biggr$_0$ , $\biggr$\frac{1}{2},\frac{3}{2}\biggr$_1$ , $\biggr$\frac{1}{2},\frac{3}{2}\biggr$_2$ , $\biggr$\frac{3}{2},\frac{3}{2}\biggr$_0$ and $\biggr$\frac{3}{2},\frac{3}{2}\biggr$_2$ .

Even when jj-coupling is technically more accurate for heavy atoms, chemists often stick to the LS notation because it’s more intuitive for discussing symmetry and spectroscopy.

Molecular term symbols

Molecular term symbols are denoted by irreducible representations of the molecule’s point group because eigenstates of the molecular Hamiltonian transform according to irreducible representations of that group.

In linear molecules, the spherically symmetric electric field experienced by an electron in an atom is replaced by a cylindrically symmetric field about the molecular axis. As a result of this cylindrical symmetry, electrons experience a non-zero torque $\boldsymbol{\mathit{\tau}}$ that causes their orbital angular momentum $\boldsymbol{\mathit{L}}$ to precess about the molecular axis (taken as the $z$ -axis).

Question

Explain why a non-zero torque is generated on the electrons.

Answer

Classically, electrons are constantly moving around the nucleus of an atom. In an isolated atom, the potential is spherically symmetric, so the force on an electron is purely radial: $\boldsymbol{\mathit{F}}=-\nabla V(r)=-\frac{dV}{dr}\hat{\boldsymbol{\mathit{r}}}$ . As a result, the torque $\boldsymbol{\mathit{\tau}}=\boldsymbol{\mathit{r}}\times\boldsymbol{\mathit{F}}$ vanishes.

In a linear molecule, however, the electronic potential is no longer spherically symmetric but cylindrically symmetric about the molecular axis. When an electron’s orbital motion is tilted relative to this axis, the force acting on the electron generally has components that are not parallel to $\boldsymbol{\mathit{r}}$ . Consequently, $\boldsymbol{\mathit{r}}\times\boldsymbol{\mathit{F}}\neq 0$ , and a non-zero torque is generated on the electrons.

To explain the precessional motion, we show that the Hamiltonian $\hat{H}$ is invariant under rotations about the $z$ -axis, but not the $x$ – and $y$ -axes. Consider the Hamiltonian of a diatomic molecule in which the electronic potential term is:

$V=-\frac{e^2}{\vert\boldsymbol{\mathit{r}}-\boldsymbol{\mathit{R}}_1\vert}-\frac{e^2}{\vert\boldsymbol{\mathit{r}}-\boldsymbol{\mathit{R}}_2\vert}$

where $\boldsymbol{\mathit{r}}$ , $\boldsymbol{\mathit{R}}_1$ and $\boldsymbol{\mathit{R}}_2$ are the position vectors of the electron, the first nucleus and the second nucleus respectively.

Using the Born-Oppenheimer approximation, the nuclear positions are fixed and a rotation operator acts only on the electronic coordinates. Let $\boldsymbol{\mathit{r}}=(x,y,z)$ , $\boldsymbol{\mathit{R}}_1=(0,0,R)$ and $\boldsymbol{\mathit{R}}_2=(0,0,-R)$ . Then $\boldsymbol{\mathit{r}}-\boldsymbol{\mathit{R}}_1=(x-0,y-0,z-R)$ and $\vert\boldsymbol{\mathit{r}}-\boldsymbol{\mathit{R}}_{1,2}\vert=\sqrt{x^2+y^2+(z\mp R)^2}=\sqrt{z^2+(z\mp R)^2}$ . Therefore, $V$ and hence $\hat{H}$ is invariant under a rotation about the $z$ -axis ( $z$ doesn’t change), but not around the $x$ – and $y$ -axes (both $x$ and $y$ changes). It follows that $[\hat{H},\hat{L}_z]=0$ , while $[\hat{H},\hat{L}_x]\neq 0$ and $[\hat{H},\hat{L}_y]\neq 0$ (see this article for details). Thus, only the projection of $\boldsymbol{\mathit{L}}$ (denoted by $\Lambda$ ) along the molecular axis is a constant of motion.

The corresponding molecular term symbol for a linear molecule is:

$^{2S+1}\Lambda_{\Omega}$

where $\Omega=\vert\Lambda+\Sigma\vert$ is the projection of the total electronic angular momentum onto the molecular axis and

Additional symmetry labels such as $g$ and $u$ (gerade and ungerade), as well as $+$ and $-$ , apply depending on the symmetry of the molecule. For example, the ground state of molecular oxygen, for which spin-orbit coupling is weak, is $^3\Sigma_g^-$ . If high-resolution spectroscopy is used, then we label the split states $^3\Sigma_{1,g}^-$ and $^3\Sigma_{0,g}^-$ .