The Hückel method is a semi-empirical method that makes additional assumptions to the 
-electron approximation in order to determine the energies of molecular orbitals in planar molecules that are conjugated.
Question
What is a semi-empirical method?
Answer
A semi-empirical method combines theoretical approximations with experimental data to derive useful parameters, such as the energy of a molecular orbital (MO).
Like the -electron approximation, the Hückel method assumes that 
valence electrons in planar conjugated organic compounds are relatively unreactive for reactions that do not involve in breaking these bonds. Furthermore, they are assumed not to interact with the valence electrons, which participate in many reactions. Consequently, the valence electrons are ignored in deriving the energies of the MOs.
To solve for the energies 
of -electron MOs, we refer to eq157 of the Hartree-Fock-Roothaan method. The total wavefunction is 
, where 
is the antisymmetriser and 
. The index 
refers to the number of carbon atoms forming the conjugated framework of the planar molecule, while 
is a real and normalised 
orbital of the 
-th carbon atom. Non-trivial solutions are given by the secular determinant:
where
is known as the Coulomb integral if 
.
is known as the resonance integral if 
.
is the normalisation expression of if .
is known as the overlap integral if .
is the eigenvalue associated with 
.
Unlike ab initio methods, the exact form of the effective Hamiltonian 
in 
is not important (see below for explanation). The additional assumptions used in the Hückel method are:
In other words, all Coulomb integrals (interaction energy) have the same value of 
, which is reasonable if all the atoms forming the conjugated framework are the same. It follows that 
for adjacent atoms is similarly a good approximation. From ab initio calculations, both and 
are negative. As non-adjacent carbons atoms are well separated in space, the conjecture that 
for non-adjacent carbons atoms and 
is also reasonable. The integral 
is a result of the normalisation of orbitals. However, 
for adjacent carbon atoms is a poor approximation because orbitals of adjacent carbon atoms are not orthogonal to one another. In reality, the overlap of orbitals of adjacent carbon atoms leads to a stabilisation (lower energy) of bonding MOs and a destabilisation (increase in energy) of antibonding MOs. Nevertheless, the relative order of the MOs along the energy axis generally remains unchanged.
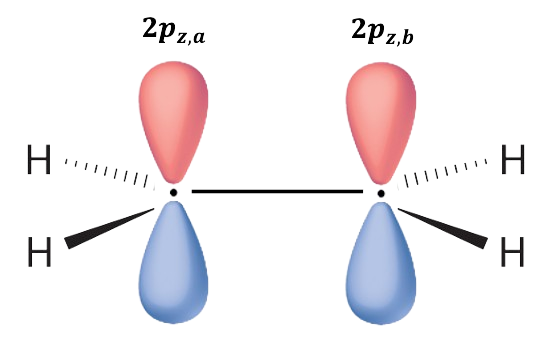
Let’s look at a simple example: ethene. The wavefunction is 
and the secular determinant is
Since the orbitals are real and is Hermitian, 
and 
. Furthermore, and we have
This implies that 
and the ground state electron configuration of the electrons in ethene is
Consequently, the Hückel method provides a quick way of predicting the number and order of a conjugated molecule’s valence MOs that likely to participate in a reaction, without explicitly specifying the Hamiltonian. The parameters and are adjusted to give the best fit to experimental data, which is why the Hückel method is considered a semi-empirical method. The total ground state electronic energy of ethene is 
.
Question
Show that i) 
when 
and 
when 
, and that ii) the normalisation constant 
of )
is 
.
Answer
i) Multiplying the eigenvalue equation =E_i(c_1\phi_1+c_2\phi_2))
by 
, integrating over all space and using the Hückel assumptions, we get
(\alpha-E_i)+2c_1c_2\beta=0)
For and , we have and , respectively.
Therefore, the occupied MO wavefunction and unoccupied MO are and )
respectively. Since the two electrons occupying lead to a stable molecule, the MO is known as the bonding MO. The higher energy MO, which obviously results in a relatively less state when occupied, is known as the antibonding MO.
ii)
^*N(\phi_1+\phi_2)d\tau=1)
=1)
Since , we have
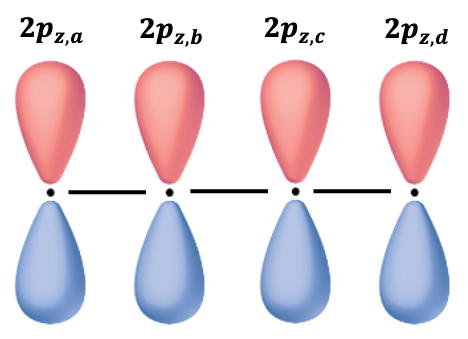
Let’s consider another molecule: 1,3-Butadiene. The secular determinant is:
The Hückel assumptions give
Using the determinant identity 
, we multiply both sides of the above equation by 
to yield
where 
.
Expanding the determinant, we have 
. The roots to the polynomial are 
and the energies of the MOs are
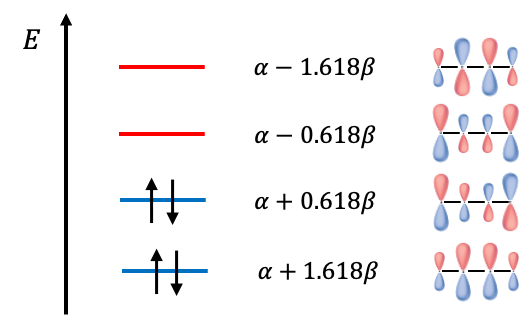
If we regard two electrons in 1,3-Butadiene as localised between carbons atoms 
and 
, and another two between carbon atoms 
and 
, we can compare the total ground state electronic energy of 1,3-Butadiene with that of two molecules of ethene. The difference of 
implies an energy stabilisation for 1,3-Butadiene that is due to the delocalisation of electrons over the length of the molecule, rather than being localised.
The general form of the wavefunction for the four MOs is 
. To determine each individual wavefunction, we apply the Hückel assumptions to eq157, giving
c_1+\beta c_2=0\;\;\;\;\;\;\;\;162)
 c_2+\beta c_3=0\;\;\;\;\;\;\;\;163)
 c_3+\beta c_4=0\;\;\;\;\;\;\;\;164)
 c_4=0\;\;\;\;\;\;\;\;165)
From eq162 and eq165, we have
Substituting eq166 in eq163 gives ^2]c_2+\beta(\alpha-E_i)c_3=0)
. When 
, we have 
.
Substituting in eq166 and comparing with eq167, 
. It follows that 
. Therefore, )
, which becomes 
after normalisation. Using the same logic, we have
For more complicated molecules, such as benzene, the Hückel method is combined with group theory to derive the wavefunctions and solve for their associated eigenvalues.