Tight-binding model

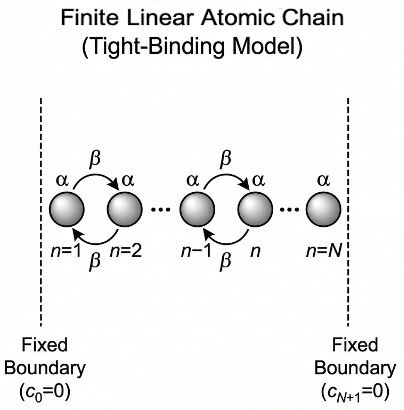
The tight-binding model incorporates the Hückel approximation to describe the electronic structure of solids by treating electrons as localised around atoms and hopping between neighbouring sites.

Consider a linear chain of $N$ identical atoms located at position $n=1,2,\cdots,N$ , with $\vert n\rangle$ representing the s-orbital of atom $n$ . According to the Hückel approximation, the Hamiltonian $\hat{H}$ is defined by two parameters:

1) $\alpha=\langle n\vert\hat{H}\vert n\rangle$ is the energy of an electron localised on a single atom.

2) $\beta=\langle n\vert\hat{H}\vert n\pm 1\rangle$ is the energy associated with an electron hopping between adjacent atoms.

3) All other matrix elements are zero.

To find the eigenvalues $E$ and eigenstates $\vert \psi\rangle$ satisfying the Schrödinger equation $\hat{H}\vert\psi\rangle=E\vert\psi\rangle$ , we adopt the linear combination of atomic orbitals (LCAO) approach, in which

$\vert \psi\rangle=\sum_{n=1}^Nc_n\vert n\rangle\;\;\;\;\;\;\;\;1$

Multiplying the Schrödinger equation on the left by the bra $\langle n\vert$ gives:

$\langle n\vert\hat{H}\vert\psi\rangle=E\langle n\vert\psi\rangle\;\;\;\;\;\;\;\;2$

Substituting eq1 into eq2, and noting that the states are orthonormal, yields:

$\sum_{m=1}^Nc_m\langle n\vert\hat{H}\vert m\rangle=E\sum_{m=1}^Nc_m\langle n\vert m\rangle=Ec_n\;\;\;\;\;\;\;\;3$

Expanding the first summation in eq3 and applying the Hückel approximation results in:

$\beta c_{n-1}+\alpha c_n+\beta c_{n+1}=Ec_n\;\;\;\;\;\;\;\;4$

Substituting the trial solution $c_n=Asin(n\theta)$ into eq4, and imposing the boundary conditions of $c_0=c_{N+1}=0$ , gives:

$\beta Asin\[(n-1)\theta\]+\alpha Asin(n\theta)+\beta Asin\[(n+1)\theta\]=EAsin(n\theta)$

This rearranges to:

$\beta A\{sin\[(n-1)\theta\]+sin\[(n+1)\theta\]\}=(E-\alpha)Asin(n\theta)$

Using the trigonometric identity $sin(A-B)+sin(A+B)=2sinAcosB$ , with $A=n\theta$ and $B=\theta$ yields:

$2\beta sin(n\theta)cos\theta=(E-\alpha)sin(n\theta)$

which simplifies to:

$E=\alpha+2\beta cos\theta\;\;\;\;\;\;\;\;5$

Since $c_{N+1}=0$ , we have $c_{N+1}=Asin\[(N+1)\theta\]=0$ . So, $(N+1)\theta=k\pi$ , which when substituted into eq5 gives:

$E_k=\alpha+2\beta cos\frac{k\pi}{N+1}\;\;\;\;\;\;\;\;6$

where $k=1,2,\cdots,N$ .

Although $k$ is an integer due to the condition $(N+1)\theta=k\pi$ , its specific range $k=1,2,\cdots,N$ in eq6 follows the fact that each eigenvalue $E_k$ is associated with one of $N$ linearly independent eigenstates $\vert\psi\rangle$ described by eq1.

Question

Show that $E_0$ and $E_{N+1}$ are trivial solutions.

Answer

If $k=0$ , then $\theta=0$ and $c_n=Asin(n\theta)=0$ everywhere, which is a trivial solution. If $k=N+1$ , then $\theta=\pi$ and $c_n$ is again zero everywhere. Therefore, the non-trivial solutions correspond to $k=1,2,\cdots,N$ .

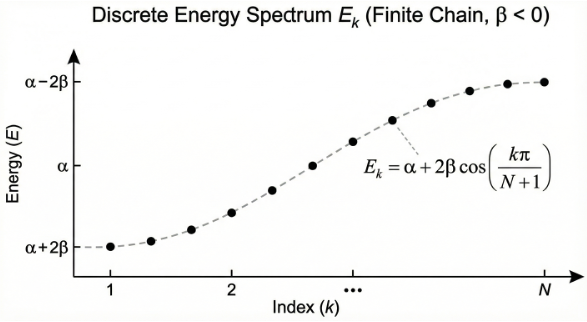
An electron localised on an atom resides in a bound state with energy measured relative to the vacuum level ( $E=0$ ). Therefore, the conventional value of $\alpha=\langle n\vert\hat{H}\vert n\rangle$ is negative. For s-orbitals, $\beta$ is also negative because $\beta=\langle n\vert\hat{H}\vert n\pm 1\rangle$ corresponds to an integral of the form (positive wavefunction) $\times$ (negative potential) $\times$ (positive wavefunction). It follows that the lower-energy states occurs when $k$ is small in eq6 (so that the cosine term is close to +1 for large $N$ ). In other words, $E_1$ and $E_N$ represent the lowest and highest energy states of the system respectively (see diagram below).