The uncertainty principle (derivation)

Heisenberg’s uncertainty principle states that the position and momentum of a particle cannot be determined simultaneously with unlimited precision.

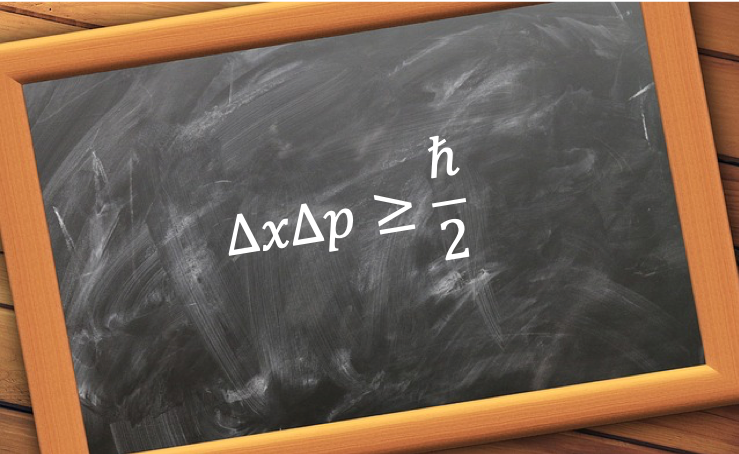
The uncertainty not only applies to the position and momentum of a particle, but to any pair of complementary observables, e.g. energy and time. In general, the uncertainty principle is expressed as:

$\Delta A\Delta B\geq \frac{1}{2}\left\vert\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle\right\vert\; \; \; \; \; \; \; \; \; 12$

where $\hat{A}$ and $\hat{B}$ are Hermitian operators and $A$ and $B$ are their respective observables.

The derivation of eq12 involves the following:

Deriving the Schwarz inequality
Proving the inequality $\left ( \Delta A \right )^{2}\left ( \Delta B \right )^{2}\geq -\frac{1}{4}\left ( \left \langle \varphi \left | \left [ \hat{A},\hat{B} \right ] \right |\varphi \right \rangle \right )^{2}$
Showing that $\left \langle \varphi \left | \left [ \hat{A},\hat{B} \right ] \right |\varphi \right \rangle =-\left \langle \varphi \left | \left [ \hat{A},\hat{B} \right ] \right |\varphi \right \rangle^{*}$

Step 1

Let

$f(\lambda)=\langle\phi-\lambda\psi\vert\phi-\lambda\psi\rangle\; \; \; \; \; \; \; \; 13$

where $\phi$ and $\psi$ are arbitrary square integrable wavefunctions and $\lambda$ is an arbitrary scalar.

Since $\langle\phi-\lambda\psi\vert\phi-\lambda\psi\rangle=\int (\phi-\lambda\psi)^{*}(\phi-\lambda\psi)d\tau=\int \vert\phi-\lambda\psi\vert^{2}d\tau\geq 0$

$f(\lambda)\geq 0\; \; \; \; \; \; \; \; \; 14$

Expanding eq13, we have

$f(\lambda)=\langle\phi\vert\phi\rangle-\lambda\langle\phi\vert\psi\rangle-\lambda^{*}\langle\psi\vert\phi\rangle+\lambda^{*}\lambda\langle\psi\vert\psi\rangle\; \; \; \; \; \; \; \; 15$

Since $\lambda$ is an arbitrary scalar, substituting $\lambda=\frac{\langle\psi\vert\phi\rangle}{\langle\psi\vert\psi\rangle}$ and $\lambda^{*}=\frac{\langle\phi\vert\psi\rangle}{\langle\psi\vert\psi\rangle}$ in eq15 gives:

$f(\lambda)=\langle\phi\vert\phi\rangle-\frac{\langle\phi\vert\psi\rangle}{\langle\psi\vert\psi\rangle}\langle\psi\vert\phi\rangle$

Substituting eq14 in the above equation and rearranging yields $\langle\phi\vert\psi\rangle\langle\psi\vert\phi\rangle \leq\langle\phi\vert\phi\rangle\langle\psi\vert\psi\rangle$ . Since $\langle\phi\vert\psi\rangle= \langle\psi\vert\phi\rangle^{*}$

$\vert\langle\psi\vert\phi\rangle\vert^{2}\leq\langle\phi\vert\phi\rangle\langle\psi\vert\psi\rangle\; \; \; \; \; \; \; \; 16$

Eq16 is called the Schwarz Inequality.

Step 2

Let $\psi=(\hat{A}-\langle A\rangle)\varphi$ and $\phi=(\hat{B}-\langle B\rangle)\varphi$ , where $\varphi$ is normalised, and $\hat{A}$ and $\hat{B}$ are Hermitian operators, which implies that $\hat{A}-\langle A\rangle$ and $\hat{B}-\langle B\rangle$ are also Hermitian operators (see this article for proof). The variance of the observable of $\hat{A}$ is

$(\Delta A)^{2}=\frac{\sum_{i=1}^{N}(\hat{A}-\langle A\rangle)^{2}}{N}=\langle(\hat{A}-\langle A\rangle)^{2} \rangle$

$=\langle \varphi\vert(\hat{A}-\langle A\rangle)[(\hat{A}-\langle A\rangle)\varphi]\rangle=\langle [(\hat{A}-\langle A\rangle)\varphi]\vert[(\hat{A}-\langle A\rangle)\varphi]\rangle=\langle\psi\vert\psi \rangle\; \; \; \; \; \; \; \; 17$

Note that the 2^nd last equality uses the property of Hermitian operators (see eq36). Similarly,

$(\Delta B)^{2}=\langle\phi\vert\phi\rangle\; \; \; \; \; \; \; \; 18$

Substituting eq17 and eq18 in eq16 results in

$(\Delta A)^{2}(\Delta B)^{2} \geq\vert \langle\psi\vert\phi\rangle\vert^{2} \; \; \; \; \; \; \; \; 19$

Let $z= \langle\psi\vert\phi\rangle$ where $z=x+iy$ . So, $\left | z \right |^{2}=x^{2}+y^{2}\geq y^{2}$ . Since $y=\frac{z-z^{*}}{2i}$ , we have $\left | z \right |^{2}\geq \left ( \frac{z-z^{*}}{2i} \right )^{2}$ , which is

$\left | \langle\psi\vert\phi\rangle\right |^{2}\geq \left ( \frac{\langle\psi\vert\phi\rangle-\langle\psi\vert\phi\rangle^{*}}{2i} \right )^{2}=-\frac{1}{4}\left (\langle\psi\vert\phi\rangle-\langle\phi\vert\psi\rangle\right )^{2}\; \; \; \;\; \; \; \; 20$

Substituting eq19 in eq20 gives

$(\Delta A)^{2}(\Delta B)^{2}\geq -\frac{1}{4}\left ( \langle\psi\vert\phi\rangle-\langle\phi\vert\psi\rangle\right )^{2}\; \; \; \; \; \; \; \; 21$

Next, we have

$\langle\psi\vert\phi\rangle= \langle (\hat{A}-\langle A\rangle)\varphi\vert (\hat{B}-\langle B\rangle )\varphi\rangle=\langle\varphi\vert(\hat{A}-\langle A\rangle)(\hat{B}-\langle B\rangle)\varphi\rangle$

$=\langle\varphi\vert\hat{A}\hat{B}\vert\varphi\rangle-\langle B\rangle\langle\varphi\vert\hat{A}\vert\varphi\rangle-\langle A\rangle\langle\varphi\vert\hat{B}\vert\varphi\rangle+\langle A\rangle\langle B \rangle\langle\varphi\vert\varphi\rangle$

$=\langle\varphi\vert\hat{A}\hat{B}\vert\varphi\rangle-\langle A\rangle\langle B \rangle \; \; \; \; \; \; \; \; 22$

Similarly,

$\langle\phi\vert\psi\rangle=\langle\varphi\vert\hat{B}\hat{A}\vert\varphi\rangle-\langle B\rangle\langle A \rangle \; \; \; \; \; \; \; \; 23$

Substituting eq22 and eq23 in eq21 yields

$(\Delta A)^{2}(\Delta B)^{2}\geq -\frac{1}{4}(\langle\varphi\vert\hat{A}\hat{B}\vert\varphi\rangle-\langle\varphi\vert\hat{B}\hat{A}\vert\varphi\rangle )^{2}$

$=-\frac{1}{4}(\langle\varphi\vert\hat{A}\hat{B}-\hat{B}\hat{A}\vert\varphi\rangle )^{2}=-\frac{1}{4}(\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle )^{2}\; \; \; \; \; \; \; \; 24$

Step 3

$\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle=\langle\varphi\vert\hat{A}\hat{B}\vert\varphi\rangle-\langle\varphi\vert\hat{B}\hat{A}\vert\varphi\rangle=\langle\hat{A}\varphi\vert\hat{B}\varphi\rangle-\langle\hat{B}\varphi\vert\hat{A}\varphi\rangle$

$=\langle\varphi\vert\hat{B}(\hat{A}\varphi)\rangle^{*}-\langle\varphi\vert\hat{A}(\hat{B}\varphi)\rangle^{*}=- \{\langle\varphi\vert\hat{A}(\hat{B}\varphi)\rangle^{*}-\langle\varphi\vert\hat{B}(\hat{A}\varphi)\rangle^{*}\}$

$=-\{\langle\varphi\vert\hat{A}(\hat{B}\varphi)\rangle-\langle\varphi\vert\hat{B}(\hat{A}\varphi)\rangle\}^{*}=-\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle^{*}\; \; \; \; \; \; \; \; 25$

We have used eq37 for the 2^nd equality and eq35 for the 3^rd equality. Substituting eq25 in one of the $\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi)\rangle$ in eq24 results in

$(\Delta A)^{2}(\Delta B)^{2}\geq\frac{1}{4} \{\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle^{*}\}\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle$