The Wigner D-matrix 
, where the total angular momentum 
is a unitary matrix that represents all rotation symmetry operations corresponding to the irreducible representations of the SU(2) group.
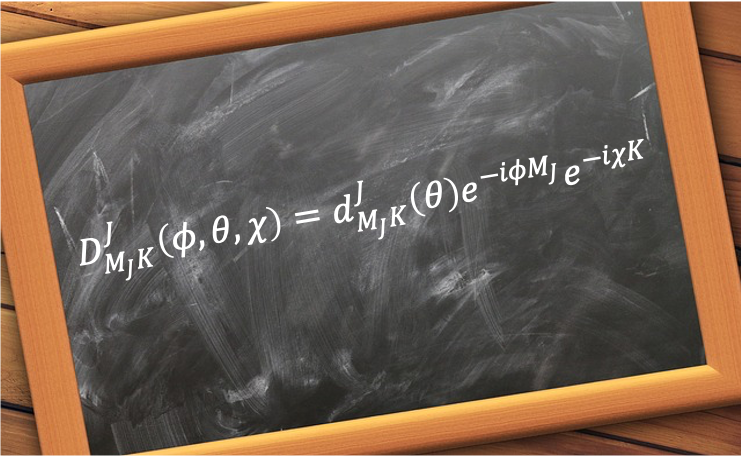
The irreducible representations of SU(2), or special unitary group of degree 2, consists of 
unitary matrices with determinant 1. They describe angular momentum transformation for particles with both integer and half-integer values of 
. In the case where is an integer, the corresponding Wigner D-matrices also represent the irreducible representations of the SO(3) group, which is the group of all proper rotations in 3D space.
As shown in the previous article, the total rotation operator )
transforms a quantum state 
with total angular momentum projection along the molecular 
-axis into a linear combination of states 
with the projection along the lab 
-axis:
\vert J,K\rangle=\sum_{M_J}D^J_{M_JK}(\phi,\theta,\chi)\vert J,M_J\rangle)
Since forms a complete orthogonal basis set for SO(3), the coefficients of , according to group theory, are the matrix elements of . Multiplying the above equation on the left by the bra 
gives the Wigner D-matrix elements:
=\langle J,M_J\vert\hat{D}(\phi,\theta,\chi)\vert J,K\rangle\;\;\;\;\;\;\;\;120)
Substituting eq115 into eq120 yields:
=\langle J,M_J\vert e^{-i\phi\hat{J}_z}e^{-i\theta\hat{J}_y}e^{-i\chi\hat{J}_z}\vert J,K\rangle\;\;\;\;\;\;\;\;121)
where is an eigenstate of 
by convention.
If 
, then 
(see this article for proof). So, 
and eq121 becomes:
=e^{-i\chi K}\langle J,M_J\vert e^{-i\phi\hat{J}_z}e^{-i\theta\hat{J}_y}\vert J,K\rangle\;\;\;\;\;\;\;\;122)
Since 
and is Hermitian, i.e. 
, we have ^{\dagger})
. It follows that
=e^{-i\chi K}(e^{i\phi M_J}\vert J,M_J\rangle)^{\dagger} e^{-i\theta\hat{J}_y}\vert J,K\rangle=d^J_{M_JK}(\theta)e^{-i\phi M_J}e^{-i\chi K}\;\;\;\;\;\;\;\;123)
where =\langle J,M_J\vert e^{-i\theta \hat{J}_y}\vert J,K\rangle)
is the Wigner small-d matrix element.
The corresponding Wigner small-d matrix 
is a single-axis, single-angle rotation operator of the SO(3) group in the basis.
)
, other than being matrix elements of Wigner D-matrices, are also rotational wavefunctions. To explain why, we refer to the great orthogonality theorem for finite groups, given by:
_{ij}\Gamma_{k^{'}}(a)_{i^{'}j^{'}}=\frac{1}{d}\delta_{ii^{'}}\delta_{jj^{'}}\delta_{kk^{'}})
where
-
_{ij})
refers to the matrix entry in 
-th row and 
-th column of the 
-th matrix of the 
-th irreducible representation.
is the order of the group, and is also the normalisation factor for the sum.
is the dimension of the irreducible representation.
The theorem can be extended to infinite groups like SO(3), with the normalised sum over group elements replaced by a normalised integral over all rotation angles 
:
}D^J_{M_JK}(R)^*D^{J^{'}}_{M^{'}_JK^{'}}(R)d\tau_r=\frac{1}{2J+1}\delta_{jj^{'}}\delta_{M_jM_j^{'}}\delta_{KK^{'}}\;\;\;\;\;\;\;\;124)
where
-
, the total volume of the SO(3) manifold (intrinsic rotation space), is the normalisation factor for the integral, i.e. }d\tau_r=\int^{2\pi}_0d\phi\int^{\pi}_0sin\theta d\theta\int^{2\pi}_0d\chi=8\pi^2)
.
(see this article for further explanation).
is a specific set of 
values.
Eq124 reveals that the functions )
are complex and orthonormal. They are eigenfunctions of and 
(in 
units), where:
=d^J_{M_JK}(\theta)\biggr\(-i\frac{\partial}{\partial\phi}e^{-i\phi M_J}\biggr\)e^{-i\chi K}=-M_JD^J_{M_JK}(R))
and
=d^J_{M_JK}(\theta)e^{-i\phi M_J}\biggr\(i\frac{\partial}{\partial\chi}e^{-i\chi K}\biggr\)=KD^J_{M_JK}(R))
Since there are infinite SO(3) irreducible representations, are associated with all possible combinations of the three rotational quantum numbers and hence all possible eigenvalues. In other words, form a complete orthonormal set of wavefunctions for symmetric rotors.
