Crystallographic restriction theorem

The crystallographic restriction theorem generally states that the rotational symmetries of a crystal are limited.

We have seen from a previous section that a lattice is formed by repeating lattice points that have the same environment. It is this fundamental geometric property of a lattice that restricts the number of rotational symmetries of a space lattice and hence the types of unit cells.

To illustrate the crystallographic restriction theorem, let’s consider a row of lattice points (indicated by the line connecting blue dots in figure I of the below diagram) that are equally spaced by the basis vector a.

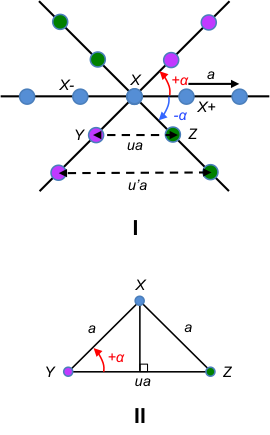
Assuming that the lattice has a rotational symmetry given by the angle $\alpha$ , a rotation about the lattice point X by + $\alpha$ , around an axis perpendicular to the plane of this page, maps the blue lattice point X- to the pink lattice point Y. Similarly, a rotation about the same lattice point X by – $\alpha$ maps the blue lattice point X+ to the green lattice point Z.

Since the rotations are symmetry operations, Y and Z are also lattice points. As mentioned in an earlier article, the lattice points in a two-dimensional lattice are described by the position vector r = ua + vb where u, v ∈ $\mathbb{Z}$ . Therefore, YZ must be a lattice vector separated by an integer multiple of a, i.e. YZ = ua + 0b or YZ = ua, where u ∈ $\mathbb{Z}$ . With reference to figure II of the above diagram,

$cos\alpha =\frac{u\textbf{\textit{a}/2}}{\textbf{\textit{a}}}=\frac{u}{2}\; \; \; \; \; \; \; (4)$

Since -1 ≤ cos $\alpha$ ≤ 1,

$-1\leq \frac{u}{2}\leq 1\; \; \; \; \Rightarrow \; \; \; \;-2\leq u\leq 2\; \; \; \;u\in \mathbb{Z}\; \; \; \; \; \; \; (5)$

Substituting eq5 in eq4, the possible values of $\alpha$ are 180^o, 120^o, 90^o, 60^o, 0^o (or 360^o). As we have assumed that a rotation of the lattice by the angle $\alpha$ transforms the lattice into a state that is indistinguishable from the starting state, the possible values of $\alpha$ correspond to 2-, 3-, 4-, 6- and 1-fold symmetry of the two-dimensional lattice.

For a space lattice in three dimensions, consider a three-dimensional lattice vector r = ua + vb + wc that is neither parallel nor perpendicular to the axis of rotation (see diagram below). A rotation by $\alpha$ maps r onto another lattice vector r’ that has the same magnitude as r. Since both r and r’ are lattice vectors, their difference r’ – r is also a lattice vector, which lies on a plane that is perpendicular to the axis of rotation.

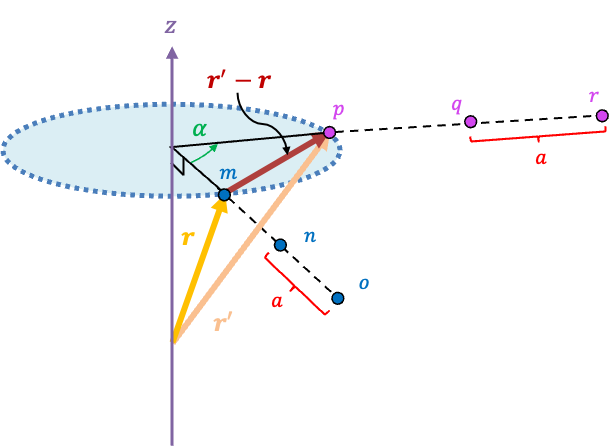
By varying the integers u, v and w, we can extend m to a row of points mno that are spaced $\vert \boldsymbol{\mathit{r'}}-\boldsymbol{\mathit{r}}\vert=a$ apart. This reduces a three-dimensional lattice proof of the crystallographic restriction theorem to a two-dimensional one, which is already given above.

We have proven the crystallographic restriction theorem with trigonometry. The proof can also be made with linear algebra (see this article).

Crystallographic restriction theorem

The crystallographic restriction theorem generally states that the rotational symmetries of a crystal are limited.

We have seen from a previous section that a lattice is formed by repeating lattice points that have the same environment. It is this fundamental geometric property of a lattice that restricts the number of rotational symmetries of a space lattice and hence the types of unit cells.

next article: Bravais lattice (2d)

Previous article: Fractional coordinates

Content page of X-ray crystallography

Content page of advanced chemistry

Main content page