The classical atomic theory is an early scientific interpretation of the atom.
Niels Bohr, a Danish physicist, introduced a model in 1911 to explain the hydrogen spectrum, which he used to derive the Rydberg formula.

He proposed that the electron of a hydrogen atom orbits around the fixed massive nucleus (see diagram below), with the coulombic force of interaction between the electron and the nucleus being balanced by the centrifugal force, i.e.
where e is the charge on the electron, ε0 is permittivity of free space, r is the radius of the orbit, me is the mass of the electron, and v is the speed of the electron.

Bohr further proposed that, for an orbit to remain stable, the angular momentum of the electron must be an integer multiple of :
where is the Planck constant. Combining eq1 and eq2 and eliminating
. we have:
Substitute eq3 back in eq2,

Question
What is angular momentum and how did Bohr arrive at the assumption for eq2?
Answer
Angular momentum is the rotational analogue of linear momentum. While the momentum of a body travelling in a straight line is proportional to its mass and velocity (p = mv), the momentum of a body revolving around a point is proportional to its mass, tangential velocity and the perpendicular distance from its tangential velocity to the point (L = mvr). Electrons, according to Bohr, orbit the nucleus at distinct radii and consequently have discrete values of angular momentum. He proposed that these radii are such that the angular momentum are integer multiples of .
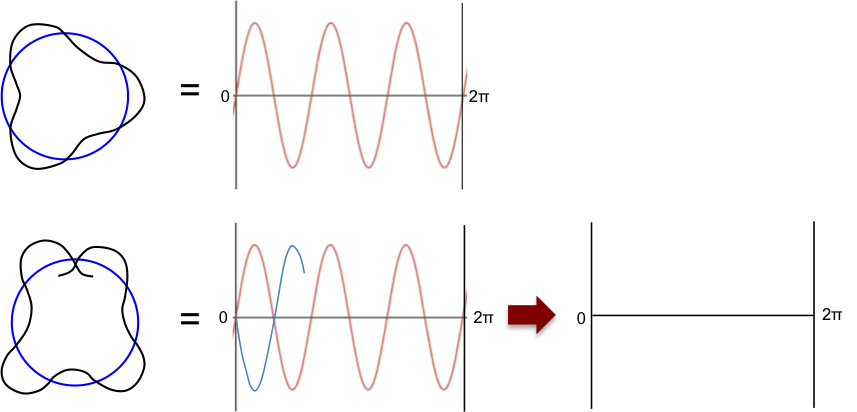
Louis de Broglie, a French physicist, subsequently reinterpreted Bohr’s model by treating electrons as waves. He proposed that an integral number of the electron’s wavelength must fit the orbit’s circumference for the orbit to be stable, i.e.
, where
. Otherwise, the orbiting wave will disappear due to destructive interference (see diagram below).
Substituting de Broglie’s formula of p = h/λ into 2πr = nλ, we have:
Substitute eq5 in eq1, we have:
which is the same as eq4 and eq3 respectively.
The total energy of the electron is:
Substitute eq3 and eq4 in eq7,
The transition energy between two states is:
At this point, Bohr assumed that an allowed transition between two states involves an electron falling from a higher energy state to a lower energy state, with the emission of a photon of energy given by the Planck relation Ep = hv = ΔE. Therefore, eq9 becomes:
where is the wavenumber of the photon.
When n1 = 1 and n2 = ∞,
where RH or R∞ is the Rydberg constant.
Even though the Bohr model has certain shortcomings, e.g. according to the model, an electron orbiting around the nucleus would constantly radiate electromagnetic energy and eventually crash into the nucleus, eq10 and eq11 were proven to be mathematically sound for the hydrogen atom using quantum mechanics.
From eq11,
where
is known as the fine-structure constant.

Question
Show that the molar mass of carbon-12, M(12C), is:
Answer
Since the relative mass of 12C is 12 unified atomic mass units,
From eq12, . Therefore,