Derivation of Stokes’ law

The derivation of Stokes’ law involves a few steps. Firstly, we shall derive the expression $\frac{\partial p}{\partial r}=\frac{\mu}{r^2sin\theta}\frac{\partial }{\partial \theta}E^2\psi$ . Substituting eq33b in eq33, we have:

$\nabla p=-\mu\nabla\times\left ( \nabla\times\textbf{\textit{u}}\right )\; \; \; \; \; \; \; (47)$

Substituting eq35b in eq47 and working out the algebra, we get:

$\nabla p=\mu\left ( \frac{1}{r^2sin\theta} \frac{\partial }{\partial \theta}E^2\psi\right )\hat{r}-\mu\left ( \frac{1}{rsin\theta}\frac{\partial }{\partial r}E^2\psi \right )\hat{\theta}$

The gradient of a function p in spherical coordinates is $\nabla p= \frac{\partial p}{\partial r}\hat{r}+\frac{1}{r}\frac{\partial p}{\partial \theta}\hat{\theta}+\frac{1}{rsin\theta}\frac{\partial p}{\partial \phi}\hat{\phi}$ . Since fluid flow is along the z-axis, $\nabla p= \frac{\partial p}{\partial r}\hat{r}+\frac{1}{r}\frac{\partial p}{\partial \theta}\hat{\theta}$ , which when compared with the above equation:

$\frac{\partial p}{\partial r}=\frac{\mu}{r^2sin\theta}\frac{\partial }{\partial \theta}E^2\psi\; \; \; \; and\; \; \; \; \frac{1}{r}\frac{\partial p}{\partial \theta}=-\frac{\mu}{rsin\theta}\frac{\partial }{\partial r}E^2\psi\; \; \; \;\; \; \; (48)$

Next, we shall show that $E^2\psi=\frac{3}{2}\textbf{\textit{u}}\frac{a}{r}sin^2\theta$ . From a previous article, $E^2=\frac{\partial ^2}{\partial r^2}+\frac{sin\theta}{r^2}\frac{\partial }{\partial \theta}\left ( \frac{1}{sin\theta}\frac{\partial }{\partial \theta} \right )$ , and so,

$E^2\psi=\frac{\partial ^2}{\partial r^2}\psi+\frac{sin\theta}{r^2}\frac{\partial }{\partial \theta}\left ( \frac{1}{sin\theta}\frac{\partial }{\partial \theta} \right )\psi\; \; \; \; \; \; \; (49)$

Substituting eq44 in eq49 and working out the algebra, we have:

$E^2\psi=\frac{3}{2}\textbf{\textit{u}}\frac{a}{r}sin^2\theta\; \; \; \; \; \; \; (50)$

Substituting eq50 in the first equation of eq48 and integrating, we have:

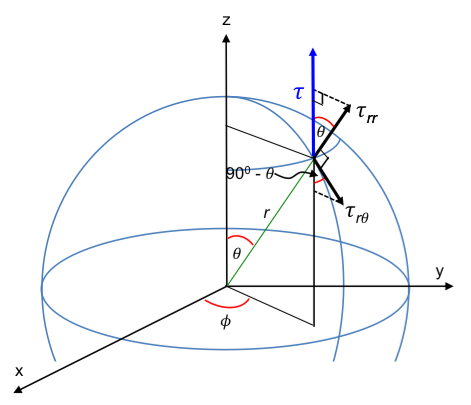
$\int_{p}^{p_\infty }dp=\int_{r}^{r_\infty }\left [ \frac{\mu}{r^2sin\theta}\frac{\partial }{\partial \theta}\left ( \frac{3}{2} \textbf{\textit{u}}\frac{a}{r}sin^2\theta\right ) \right ]dr$

$p=p_\infty -\frac{3\mu\textbf{\textit{u}}a}{2r^2}cos\theta\; \; \; \; \; \; \; (51)$

With reference to the diagram above, the stress τ on the sphere in the z-direction is given by the sum of the projections of τ_rr and τ_rθon the z-axis:

$\tau=\tau_{rr}cos\theta+\left [ -\tau_{r\theta}cos\left ( 90^o-\theta \right ) \right ]$

$\tau=\tau_{rr}cos\theta-\tau_{r\theta}sin\theta\; \; \; \; \; \; \; (52)$

From the articles on constitutive relation, $\sigma_{ij}=-p\delta_{ij}+\mu\left ( \frac{\partial u_i}{\partial x_j} +\frac{\partial u_j}{\partial x_i}\right )$ . So,

$\tau_{rr}=-p+2\mu\frac{\partial u_r}{\partial r}\; \; \; \; \; \; \; (53)$

$\tau_{r\theta}=\mu\left ( r\frac{\partial }{\partial r}\frac{u_\theta}{r}+\frac{1}{r}\frac{\partial u_r}{\partial \theta} \right )\; \; \; \; \; \; \; (53a)$

Question

Show that $\tau_{r\theta}=\mu\left ( r\frac{\partial }{\partial r}\frac{u_\theta}{r}+\frac{1}{r}\frac{\partial u_r}{\partial \theta} \right )$ .

Answer

We need to convert the term $\left ( \frac{\partial u_i}{\partial x_j} +\frac{\partial u_j}{\partial x_i}\right )$ in $\sigma_{ij}=-p\delta_{ij}+\mu\left ( \frac{\partial u_i}{\partial x_j} +\frac{\partial u_j}{\partial x_i}\right )$ , which is in Cartesian coordinates, to spherical coordinates. Let i =1 and j = 2,

$\tau_{12}=\mu\left ( \frac{\partial u_1}{\partial x_2}+\frac{\partial u_2}{\partial x_1} \right )\; \; \; \; \; \; \; (53b)$

In Cartesian coordinates, $\nabla=\hat{x_1}\frac{\partial }{\partial x_1}+\hat{x_2}\frac{\partial }{\partial x_2}+\hat{x_3}\frac{\partial }{\partial x_3}$ and $\textbf{\textit{u}}=u_1\hat{x_1}+u_2\hat{x_2}+u_3\hat{x_3}$ . So,

$\left ( \frac{\partial u_1}{\partial x_2}+\frac{\partial u_2}{\partial x_1} \right )=\left ( \hat{x_2}\cdot \nabla \right )\left ( \textbf{\textit{u}}\cdot \hat{x_1}\right )+\left ( \hat{x_1}\cdot \nabla \right )\left ( \textbf{\textit{u}}\cdot \hat{x_2}\right )$

Since $\left ( \hat{x_2}\cdot \nabla \right )$ and $\left ( \hat{x_1}\cdot \nabla \right )$ are scalars, we can rewrite the above as:

$\left ( \frac{\partial u_1}{\partial x_2}+\frac{\partial u_2}{\partial x_1} \right )=\left [ \left ( \hat{x_2}\cdot \nabla \right )\textbf{\textit{u}}\right]\cdot \hat{x_1}+\left [ \left ( \hat{x_1}\cdot \nabla \right )\textbf{\textit{u}}\right ] \cdot \hat{x_2}\; \; \; \; \; \; \; (53c)$

We can now replace the orthogonal Cartesian basis vectors with orthogonal spherical basis vectors in eq53c:

$\left ( \frac{\partial u_1}{\partial x_2}+\frac{\partial u_2}{\partial x_1} \right )=\left [ \left ( \hat{\theta}\cdot \nabla \right )\textbf{\textit{u}}\right]\hat{r}+\left [ \left ( \hat{r}\cdot \nabla \right )\textbf{\textit{u}}\right ] \hat{\theta}$

In spherical coordinates, $\nabla=\frac{\partial }{\partial r}\hat{r}+\frac{1}{r}\frac{\partial }{\partial \theta}\hat{\theta}+\frac{1}{rsin\theta}\frac{\partial }{\partial \phi}\hat{\phi}$ and $\textbf{\textit{u}}=u_r\hat{r}+u_\theta\hat{\theta}+u_\phi \hat{\phi}$ . So, working out the algebra and using the identities $\frac{\partial \hat{r}}{\partial \theta}=\hat{\theta}$ , $\frac{\partial \hat{\theta}}{\partial \theta}=-\hat{r}$ and $\frac{\partial \hat{\phi}}{\partial \theta}=0$ , the above equation becomes:

$\left ( \frac{\partial u_1}{\partial x_2}+\frac{\partial u_2}{\partial x_1} \right )=r\frac{\partial }{\partial r}\left ( \frac{u_\theta}{r} \right )+\frac{1}{r}\frac{\partial u_r}{\partial \theta}\; \; \; \; \; \; \; (53d)$