Charge balance equations

Charge balance equations are derived using the concept of electroneutrality, where the sum of positive charges equals to the sum of negative charges in a solution. Such equations are useful for analysing acid-base equilibria and formulating complex acid-base titration equations.

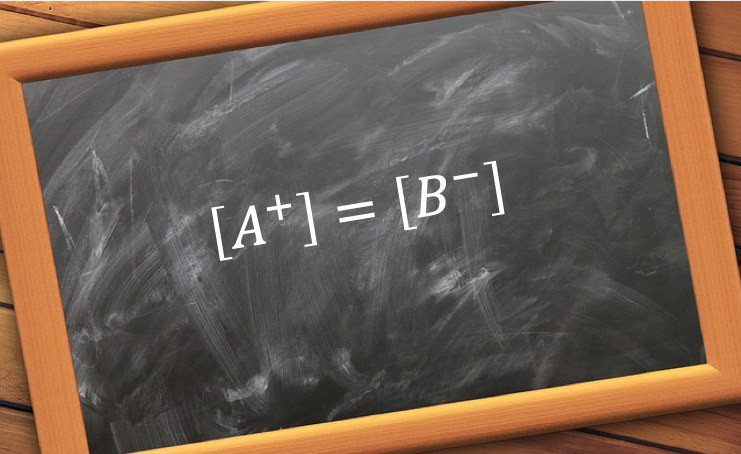
Consider a solution containing water, a strong acid of concentration C_aand a strong base of concentration C_bwith the following equilibria:

$H_2O(l)\rightleftharpoons H^+(aq)+OH^-(aq)$

$HA(aq)\rightleftharpoons H^+(aq)+A^-(aq)$

$BOH(aq)\rightleftharpoons B^+(aq)+OH^-(aq)$

With reference to charge balance of the above equilibria, the sum of the number of moles of cations H⁺ and B⁺ must equal to that of anions A^– and OH^–. As the volume is of the solution is common to all ions,

$[H^+]+[B^+]=[OH^-]+[A^-]$

When formulating charge balance equations for aqueous compounds with multiple equilibria, we need to account for every charged species on the LHS of a particular equilibrium, which can be complicated. To avoid mistakes, select equilibria where species on the LHS are neutral. For example, equilibria for a diprotic acid can be presented in the following ways:

$H_2A(aq)\rightleftharpoons H^+(aq)+HA^-(aq)$

$HA^-(aq)\rightleftharpoons H^+(aq)+A^{2-}(aq)$

$H_2A(aq)\rightleftharpoons 2H^+(aq)+A^{2-}(aq)$

Select the first and third equilibria, i.e. we can imagine part of the initial number of moles of H₂A dissociating into H_a⁺ and HA^– with the remaining part of the initial number of moles of H₂A dissociating into 2H_b⁺ and A^2-. For the first equilibria, the charge balance is