Monoprotic strong acid versus monoprotic strong base

What is the formula of the titration curve of a monoprotic strong acid versus a monoprotic strong base?

Consider a solution containing water, a strong acid (analyte) of concentration C_aand a strong base of concentration C_bwith the following equilibria:

$H_2O(l)\rightleftharpoons H^+(aq)+OH^-(aq)$

$HA(aq)\rightleftharpoons H^+(aq)+A^-(aq)$

$BOH(aq)\rightleftharpoons B^+(aq)+OH^-(aq)$

With reference to charge balance of the above equilibria, the sum of the number of moles of cations H⁺ and B⁺ must equal to that of anions A^– and OH^–. As the volume is of the solution is common to all ions,

$[H^+]+[B^+]=[OH^-]+[A^-]\; \; \; \; \; \; \; \; (1)$

Assume that the strong acid is fully ionised in water, at any point of the titration, the number of moles of A^– must equal to the initial number of moles of HA. As the change in volume of the solution is common to all ions,

$[A^-]=\frac{C_aV_a}{V_a+V_b}\; \; \; \; \; \; \; \; (2)$

where V_a and V_b are the volume of acid in the solution and the volume of base in the solution respectively.

Similarly, assuming that the strong base is fully ionised in water, at any point of the titration, the sum of the number of moles of B⁺ must equal to the number of moles of BOH added to the solution. As the change in volume of the solution is common to all ions,

$[B^+]=\frac{C_bV_b}{V_a+V_b}\; \; \; \; \; \; \; \; (3)$

Substitute eq2, eq3, K_w= [H⁺][OH^–] and [H⁺] = 10^-pH in eq1

$10^{-pH}+\frac{C_bV_b}{V_a+V_b}=\frac{K_w}{10^{-pH}}+\frac{C_aV_a}{V_a+V_b}\; \; \; \; \; \; \; \; (4)$

Eq4 is the complete pH titration curve for a monoprotic strong acid versus monoprotic strong base system. We can input it in a mathematical software to generate a curve of pH against V_b. For example, if we titrate 10 cm³ of 0.200 M of HCl with 0.100 M of NaOH, we have the following:

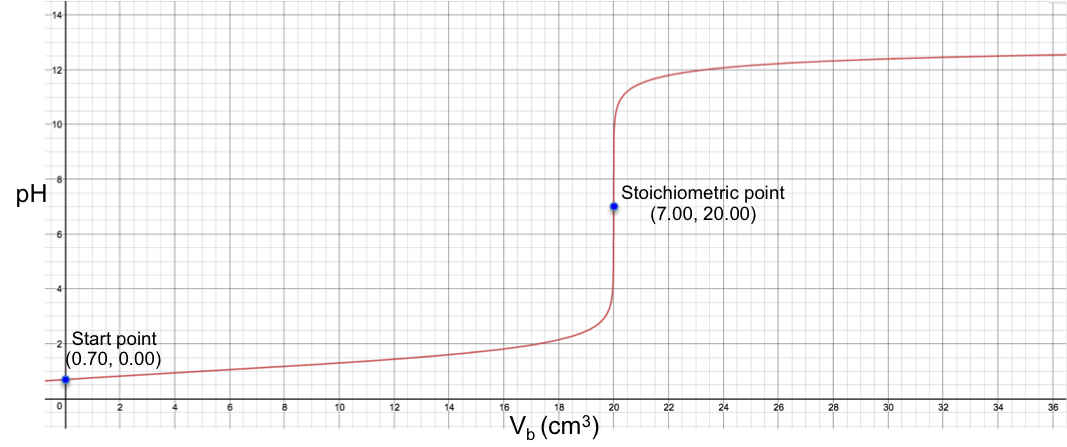
To understand the sharp change in pH near the stoichiometric point versus the change in V_b, we assume that one drop of base is about 0.05 cm³ and substitute 19.95 cm³, 20.00 cm³ and 20.05 cm³ into eq4. The respective pH just before and just after the stoichiometric point (SP) are:

	One drop before SP	SP	One drop after SP
Volume, cm³	19.95	20.00	20.05
pH	3.78	7.00	10.22

The data shows that just two drops of base cause a drastic change of 6.44 in pH before and after the stoichiometric point. We can therefore use many different indicators that work within the range of the change in pH at the stoichiometric point to monitor the titration. Furthermore, we can derive the gradient equation for a monoprotic strong acid versus monoprotic strong base titration and investigate the inflexion point at pH 7 by rearranging eq4 as:

$10^{-2pH}+\frac{C_bV_b}{V_a+V_b}10^{-pH}-\frac{C_aV_a}{V_a+V_b}10^{-pH}-K_w=0$

and finding $\frac{dpH}{dV_b}$ by implicit differentiation to give:

$\frac{dpH}{dV_b}=\frac{(C_bV_a+C_aV_a)}{ln10(V_a+V_b)[10^{-pH}2(V_a+V_b)+C_bV_b-C_aV_a]}$

At the stoichiometric point, C_bV_b – C_aV_a= 0 for a monoprotic acid-base reaction and the above equation becomes

$\frac{dpH}{dV_b}=\frac{(C_bV_a+C_aV_a)}{10^{log[H^+]}ln100(V_a+V_b)^2}$

Since [H⁺] = 10^-7 M at the stoichiometric point for a strong acid versus strong base titration, the denominator of the above equation is a very small number and hence the gradient of the pH versus curve, or , is a very large value (computed to be 7238.2 cm^-3), making at angle of 89.99^o with the horizontal, i.e. a vertical line.

Question

How do we differentiate 10^-2pH implicitly?

Answer

Let u = 10^-2pHand use the chain rule $\frac{du}{dx}=\frac{du}{dy}\frac{dy}{dx}$ where y = pH and x = V_b. The result is $-10^{-2pH}2ln10\frac{dpH}{dV_b}$ .

Monoprotic strong acid versus monoprotic strong base

Question

Answer

next article: Monoprotic weak acid versus monoprotic strong base

Previous article: overview

Content page of complete ph titration curve

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply