IR drop

IR drop in electrochemistry is the voltage drop due to the resistance of the analyte (and the internal KCl solution if a calomel or AgCl electrode is used) in a close circuit.

In the previous article regarding pH measurement, which involves potentiometry, no net current flows in the circuit. When a current flows, e.g. in coulometry and electrogravimetry, we have to consider two effects:

- IR drop
- Overpotential

We can represent IR drop as an internal resistance of a battery in the following circuit diagram:

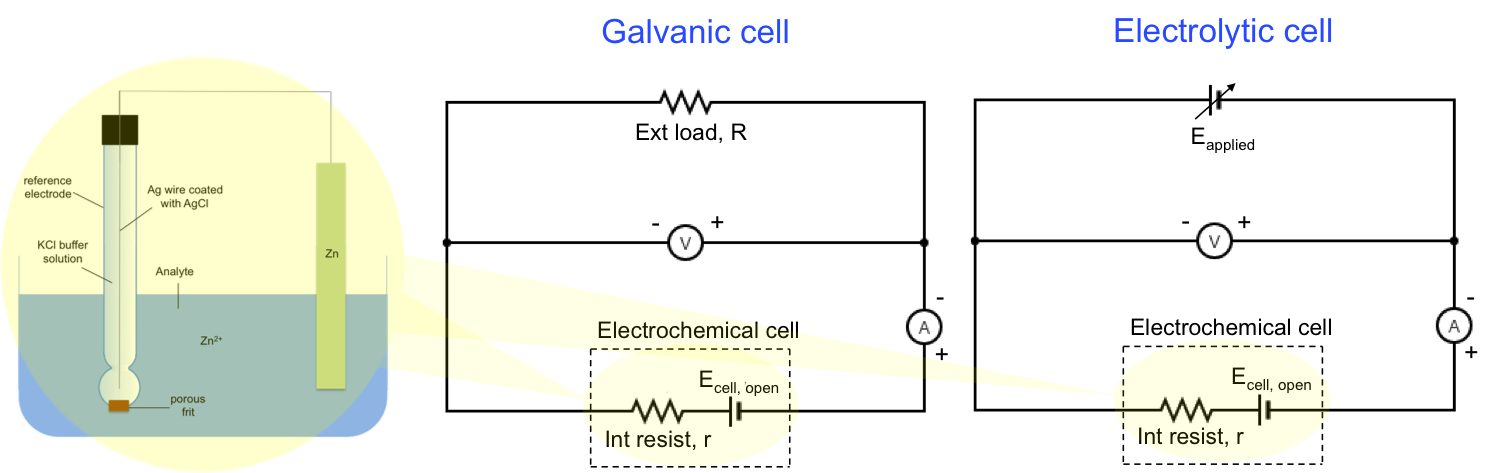
The general equation for a galvanic cell is:

$E_{galvanic}=IR=E_{cell,open}-Ir\; \; \; \; \; \; \; \; 32$

where E_cell,_open = E_R – E_L.

Eq32 when applied to a Zn electrochemical cell gives the following values:

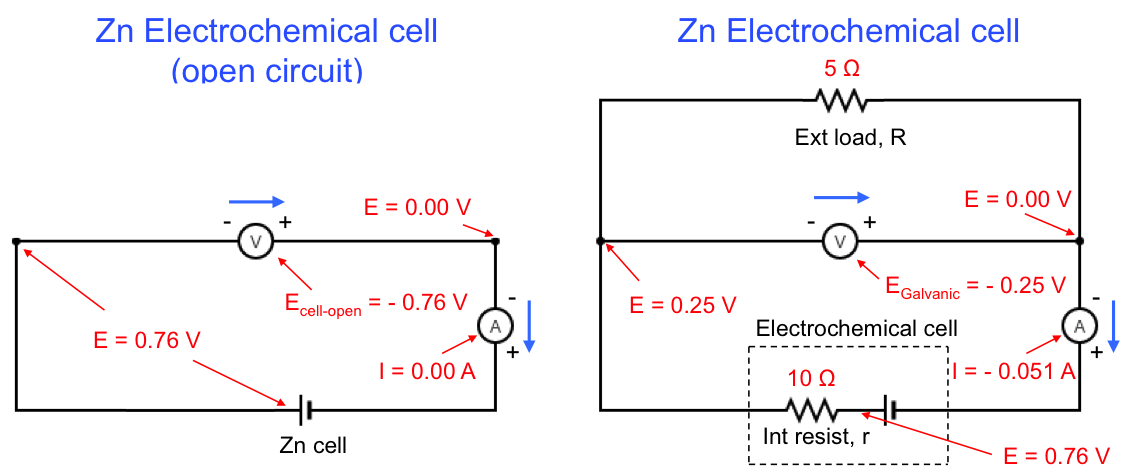
E_{cell, open} and E_galvanic for the above example are recorded as negative values by the voltmeters because of the way the terminals of the voltmeters are connected to the respective circuits. From eq32, $\left | E_{galvanic} \right |$ is always less than $\left | E_{cell,open} \right |$ .

For an electrolytic cell,

$E_{applied}=E_{cell,open}-Ir\; \; \; \; \; \; \; \; 33$

If no current is flowing in the electrolytic cell, eq33 reduces to E_applied= E_{cell, open}. For electrolysis to proceed, $\left | E_{applied} \right |>\left | E_{cell,open} \right |$ . For example, the variation of E_applied for the electrolytic reduction of Zn²⁺ is illustrated by the following diagram:

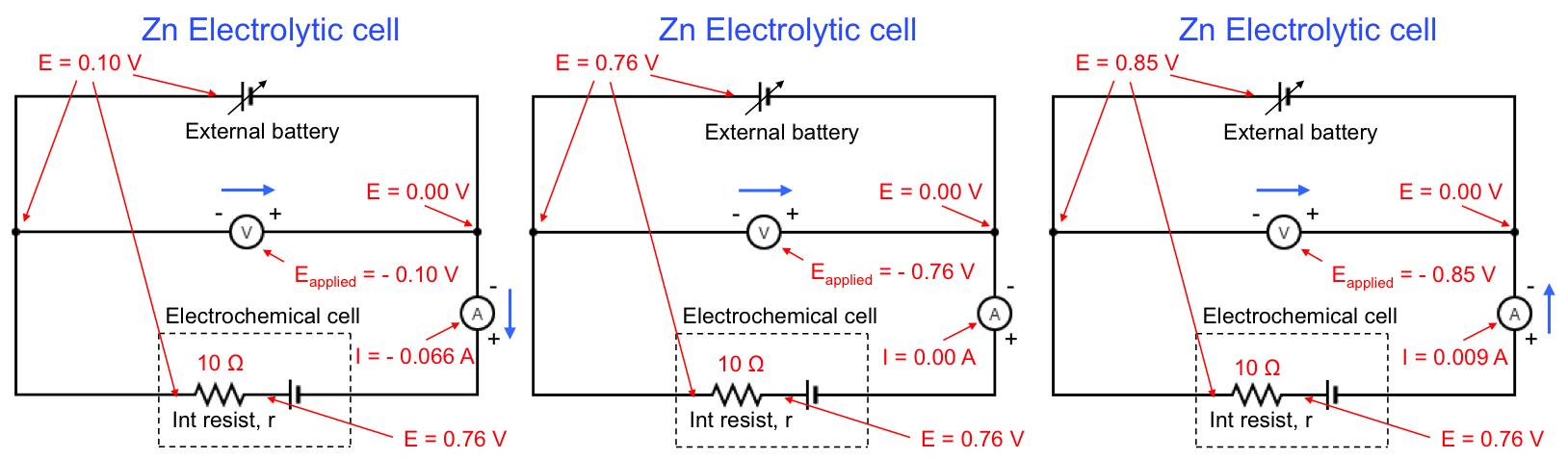
Once again, E_applied for the above example is recorded as a negative value by the voltmeter because of the way the voltmeter is connected to the circuit.

Question

With reference to the above electrochemical cell that is composed of a saturated AgCl reference electrode, a Zn working electrode and a 0.5 M Zn²⁺ electrolyte at rtp, what external voltage must be applied to generate an electrolytic current of 3 mA if the internal resistance is 10 Ω. What is the IR drop?