The transition state theory provides a theoretical way to calculate the pre-exponential factor A and the activation energy Ea, and therefore the rate constant k of an elementary chemical reaction. This is in contrast with the Arrhenius equation, where A and Ea are obtained empirically. The theory is based on statistical thermodynamics and can be illustrated for a gas-phase bimolecular reaction using the following assumptions:
1) The reacting system, expressed as , proceeds along an energy path that includes a point of highest potential energy called the saddle point, where a distinct species known as the activated complex
is formed. The conversion of the activated complex to the product P can be seen as an asymmetric vibrational stretch:
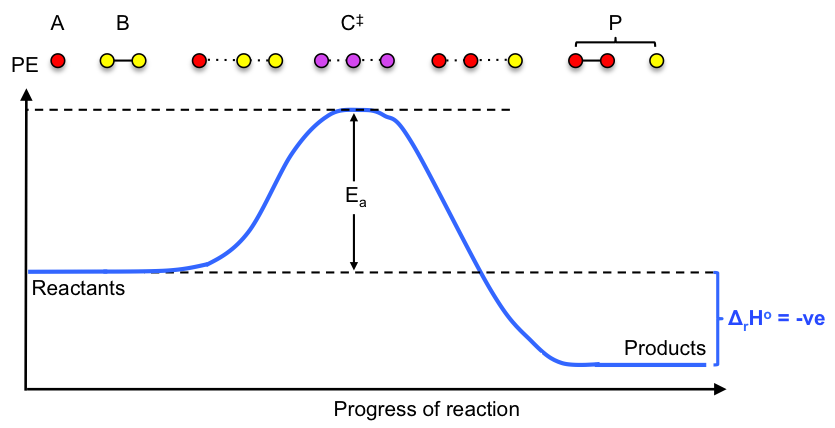
2) A rapid pre-equilibrium is established between the activated complex and the reactants: .
3) The rate of the reaction is attributed to the rate-determining step, which is the rate of conversion of the activated complex to the product: , where
is proportional to the vibrational frequency
of the activated complex.
The expression for the gas-phase rapid equilibrium from assumption 2 is:
which in terms of molar concentration is:
Substitute eq1 in the rate equation , ,
In general, the equilibrium constant, when written in terms of standard molar partition functions, is where
is the respective stoichiometric coefficient of the species. For our bimolecular reaction,
where .
The activated complex in our example is a linear molecule with N = 3 atoms and therefore has 3N – 5 = 4 modes of vibration (2 bending, 1 symmetric stretch and 1 asymmetric stretch). The standard molar partition function for the activated complex is the product of the partition functions of different modes of motion: , which we can rewrite in the form:
, where
. The standard molar partition function for the asymmetric vibration is
, where
is the vibrational frequency that leads to the conversion of the activated complex to the product. Assuming
,
. Therefore,
Substitute eq3 in eq2
where
Substitute eq4 in the rate constant equation
From assumption 3, is proportional to the vibrational frequency
of the activated complex,
where is the proportionality constant called the transmission coefficient, which accounts for the notion that not every oscillation of the activated complex leads to its conversion to the product.
Substitute eq6 in eq5,
The standard Gibbs energy is . By analogy, we define the standard Gibbs activation energy as
, which we shall substitute in eq7,

Question
Is the expression for standard Gibbs activation energy still valid when the equilibrium constant now excludes the factor ?
Answer
It is an approximation that we make, which delivers an expression for the rate constant that is in good agreement with experimental values.
Eq7 and eq8 are different forms of the Eyring equation. Substitute eq8 in the definition of activation energy and differentiate, noting that
and
are standard states, which are temperature-independent, we have
Substitute eq9 in eq8
Comparing eq10 and the Arrhenius equation,
Repeating all the above steps for a gas-phase unimolecular reaction, we arrive at an activation energy of instead of eq9. Therefore, the transition state theory predicts that the activation energy for a gas-phase elementary reaction is
where for a unimolecular reaction and
for a bimolecular reaction.
