The 1-D classical wave equation is a mathematical description of one-dimensional waves that occur in classical physics. To derive the equation, we consider a vibrating string of mass density in a 2-dimensional plane, where
is the change in mass of the string
per the change in unit length of the string.
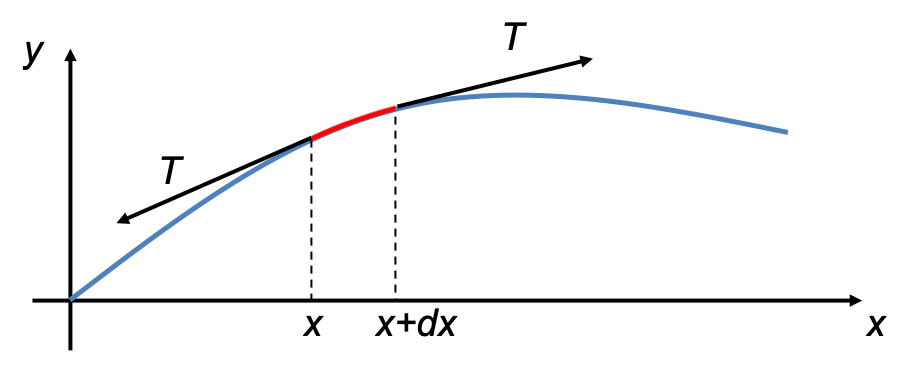
The diagram above shows that the string has been displaced from its relaxed length. When this happens, atoms or molecules within the string are pulled apart and gain potential energy. An associated restoring force called tension therefore arises in the string. As the string can be perceived as being composed of small interconnected segments, with each segment pulling adjacent segments and being pulled upon by adjacent segments, we have, for a particular segment (shown in red in the above diagram), 2 tension vectors of equal magnitude acting at its ends. Since the vectors are tangent to the curve and point in opposite directions, they do not add to zero. Ignoring the effects of gravity, the resultant vector is the restoring force acting on the segment. This restoring force (represented by the red vector in the diagram below) is approximately vertical if the amplitude of the wave is small:
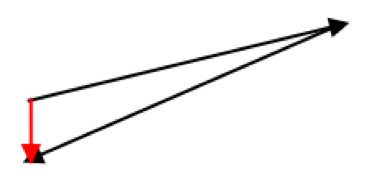
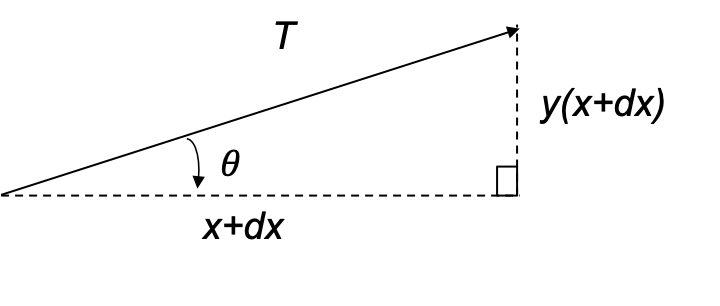
Next, we shall analyse the vertical components of forces acting on the segment. The vertical component of at
is
, and the gradient of
at
is
.
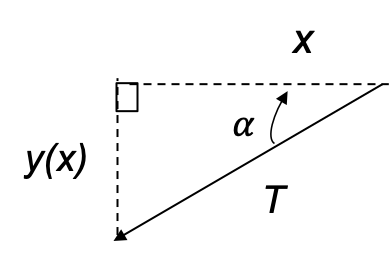
For small angles, and so,
and
. Combining the 2 equations, we have
. Similarly, for
at
, we have
. Therefore, the net vertical force
is:
Substituting in the above equation, we have
, which is then substituted with
and
to give
Since is a function of position
and time
, we replace the derivatives with partial derivatives:
For the wave equation to be applicable to both standing and travelling waves, the wavefunction should take the form of where
is wavelength and
is the velocity of the travelling wave (if
,
reduces to a standing wave). Substituting
into eq52, we have
and
. Therefore,
, which when substituted in eq52, gives
Eq53 is the 1-dimensional classical wave equation.