The Biot-Savart law is an equation describing the magnetic field generated by a current segment.
Consider a point in the vicinity of a wire carrying a current
(see diagram below).
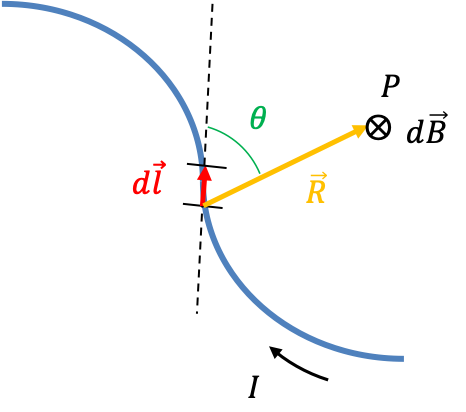
The magnitude of represents the amount of charges flowing through the wire (blue line). This implies that the amount of charges in an infinitesimal length of the wire
is proportional to
. Since the magnetic field
at
is generated by the amount of moving charges in the wire, we have
, or rather
because
is due to component of
that is perpendicular to
(use right-hand rule to visualise).
The magnetic flux generated by radiates spherically outward from every point along the infinitesimal length of the wire. For a particular
in a segment
, the amount of magnetic field lines radiated is a constant. As
increases, the surface area of the sphere becomes bigger. Therefore, the radiation passing through
must be proportional to the unit area of the sphere at
, i.e.
, where
is the unit vector in the direction of
. Finally, we would expect
to vary according to the material of the wire and the medium of the space between the wire and
. If we assume the wire to have negligible resistance and that the system is in a vacuum, we have
where is called the vacuum permeability or magnetic permeability of free space, and it represents the proportionality constant for the measurement of
at
in a vacuum.
The scalar form of eq150 is
The total field at is
Eq150, eq151 and eq152 are different forms of the Biot-Savart law.
If the wire is a circle, the direction of at
is determined by the right hand rule and is perpendicular to the plane formed by
and
, where the angle
between
and
is
(see diagram below).
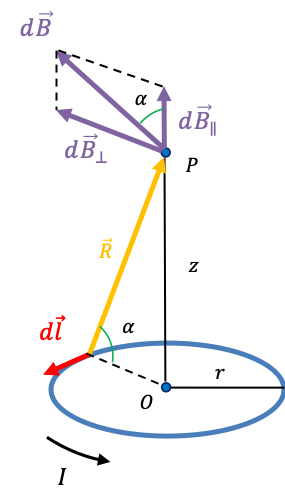
From eq151,
Let’s analyse the components of . If we sum all the vectors of
at
from all current elements around the wire, they cancel out. The vectors of
at
, however adds. Therefore, in scalar form,
, where
, which when combined with eq153 gives
Since and
, eq154 becomes
and
Substituting in the above equation
For the case of at point
, we have
, which is the length
, equals to zero. So,
For the case of , eq155 becomes
, where
. Substitute eq60 and eq61 in
,
Eq156 and eq157 are useful in constructing the orbit-orbit coupling term and the spin-orbit coupling term of the Hamiltonian.