Thomas precession is a relativistic kinematic correction to the spin-orbit coupling Hamiltonian.
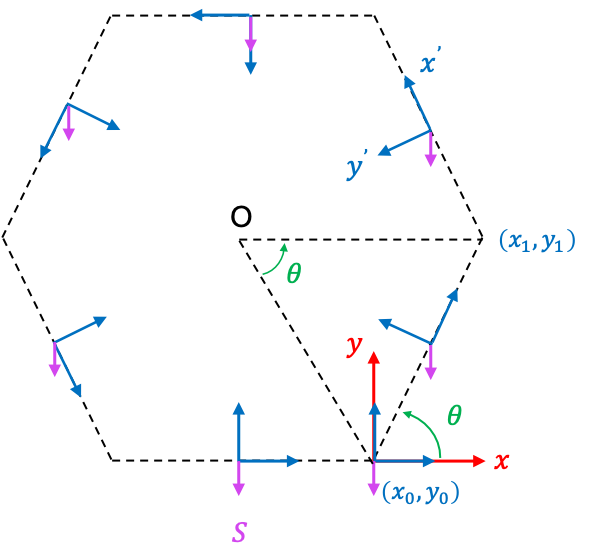
Consider an electron orbiting counter-clockwise around a nucleus at O along the path of a regular -sided polygon in the
-plane (see diagram above). At
, the nucleus sees the electron making a turn at
at an angle
. At subsequent vertices, the nucleus sees the electron turning at the same angle before arriving back to
.
In the rest frame of the electron (denoted by blue axes), becomes
due to length contraction along the direction of travel, and the electron sees itself turning at angle of
at
, where
. At subsequent vertices, the electron sees the same turning angle before arriving back to
. Substituting
in
, we have
. In the limit of large
, the polygon approaches a circle with each turning angle being very small. Using the small-angle approximation,
. According to the nucleus and the electron, each turn corresponds to
and
respectively. So, after completing a full orbit, the electron sees itself turning an angle of
.
In the rest frame of the nucleus (denoted by red axes), the orientation of the spin axis of the electron remains unchanged (just like the spin axis of the earth being constant from the sun’s perspective). However, in the rest frame of the electron, the spin axis of the electron appears to rotate clockwise. After a completing a full orbit, the change in the orientation of
is
. Since the rate of precession is defined as the rate of change in orientation of the rotational axis of a rotating body, the rate of
, called the Thomas precession, is
where ,
and
is the period of the orbit.
Substitute and eq58, where
, in eq255 (note that the radius is perpendicular to the path of travel and is not contracted, and therefore common to both nucleus and electron),
. Since
, we have
. Let
in the binomial series
. We have
or
Substitute and eq59, where
, in eq256