A representation of a group is a collection of square matrices that multiply according to the multiplication table of the group.
Consider the multiplication table for the point group :
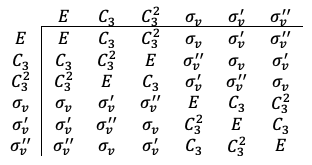
Clearly, the collections of matrices
and
are representations of the
point group because they multiply according to the above multiplication table:
An example of a representation of the point group consisting of
matrices is:
It is easy to verify that the elements of multiply according to the multiplication table of
.
These three representations of can be summarised as follows:
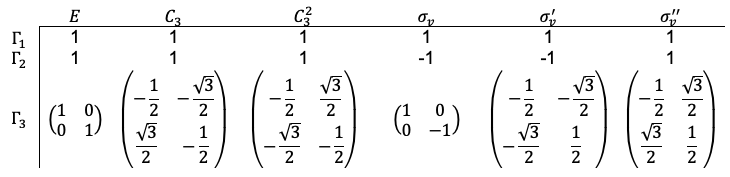

Question
Show that there are three classes for the point group.
Answer
This is easily accomplished by inspecting the elements of and noting that group elements of the same class have the same trace.
The dimension of a representation refers to the common order of its square matrices, e.g. the dimensions of and
are 1 and 2 respectively. A particular element of a representation is denoted by
, where
refers to the representation and
refers to the corresponding symmetry operator. For example,
. The matrix element of a particular element of a representation is denoted by
, e.g.
.
There are other representations of the point group, e.g.
with the following elements:

If we inspect these matrices, we realise that they are of the same form, in the sense that we can group the matrix elements into submatrices that lie along the diagonals as illustrated. We call such submatrices: blocks, and the matrices containing blocks along their diagonals: block diagonal matrices.
The consequence of the submatrices in each of the matrices being isolated by zeros is that the smaller submatrices in the multiplication of any two
matrices do not interfere with the larger submatrices. Since the collection of elements in the 1×1 blocks is the same as the collection of elements of
, and the 2×2 submatrices of the bigger blocks are the same as the collection of elements of
, we can conclude that the collection of the
matrices multiply according to the multiplication table of
without actually having to work out all the multiplications.
Another consequence of the way block diagonal matrices multiply with one another is that an infinite number of representations can be formed by adding elements of and
to the matrices of
to form larger matrices. For example, the addition of the elements of
to the
matrices gives
, with the following elements:

We call this matrix operation of adding blocks to form a larger block diagonal matrix: direct sum, which is denoted by the symbol . So,
and
.
With an infinite number of representations, we have to figure out which handful of representations of a group is sufficient for classifying molecules by symmetry and for analysing molecular properties. To do so, we first need to understand the difference between a reducible representation and an irreducible representation.