Projection operator (group theory)

A projection operator is used to construct a linear combination of a set of basis functions that spans an irreducible representation of a point group $G$ .

Using eq55, we can write

$R_{\alpha}f_l^p=\sum_{k=1}^m\Gamma_p(\alpha)_{kl}f_k^p\;\;\;\;\;\;\;\;90$

where $R_{\alpha}$ is the $\alpha$ -th symmetry operation of $G$ , $f_k^p$ is a set of $k$ basis functions of the $p$ -th irreducible representation $\Gamma$ of $G$ , and $\Gamma_p(\alpha)_{kl}$ is the $k$ -th row and $l$ -column matrix entry of $\Gamma_p(\alpha)$ .

Multiplying eq90 by $\Gamma_q^*(\alpha)_{ij}$ and sum over $\alpha$ ,

$\sum_{\alpha}^{\vert G\vert}\Gamma_q^*(\alpha)_{ij}R_{\alpha}f_l^p=\sum_{k=1}^mf_k^p \sum_{\alpha}^{\vert G\vert}\Gamma_q^*(\alpha)_{ij}\Gamma_p(\alpha)_{kl}$

Substituting eq20a in the above equation,

$\sum_{\alpha}^{\vert G\vert}\Gamma_q^*(\alpha)_{ij}R_{\alpha}f_l^p=\sum_{k=1}^mf_k^p\frac{\vert G\vert}{d_q}\delta_{ik}\delta_{jl}\delta_{pq}=\frac{\vert G\vert}{d_q}\delta_{jl}\delta_{pq}f_i^p\;\;\;\;\;\;\;91$

$P_{ij}^qf_l^p=\delta_{jl}\delta_{pq}f_i^p\;\;\;\;\;\;\;92$

where $P_{ij}^q=\frac{d_q}{\vert G\vert}\sum_{\alpha}^{\vert G\vert}\Gamma_q^*(\alpha)_{ij}R_{\alpha}$ .

$P_{ij}^q$ is a linear combination of the symmetry operators $R_{\alpha}$ with coefficients that are entries of the matrix representations of $\Gamma_q^*(\alpha)$ . If $j=l$ and $p=q$ ,

$P_{il}^qf_l^q=f_i^q\;\;\;\;\;\;\;93$

We call $P_{ij}^q$ the projection operator, which generates a basis $f_{i}^q$ of the irreducible representation $\Gamma_q$ from another basis $f_{l}^q$ of $\Gamma_q$ . The significance of this is that if we know one member of a set of basis functions of an irreducible representation, then we can project all the other members of the set.

Question

Using eq93 and the general function $f=xz+yz+z^2$ , show that the basis functions $xz$ and $yz$ belong to the degenerate irreducible representation $\Gamma_E$ of the point group $C_{3v}$ .

Answer

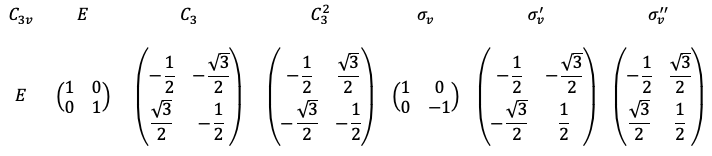
For $i=l=1$ ,

$P_{11}^Ef=\frac{2}{6}\biggr\[ \hat{E}f+\biggr$-\frac{1}{2}\biggr$\hat{C}_3f+\biggr$-\frac{1}{2}\biggr$\hat{C}_3^2f+\hat{\sigma}_v+\biggr$-\frac{1}{2}\biggr$\hat{\sigma}_v^{'}f+\biggr$-\frac{1}{2}\biggr$\hat{\sigma}_v^{''}f \biggr\]$

Substituting the values of this table into the above equation and simplifying, we have $P_{11}^Ef=xz$ . If we repeat the procedure for $i=l=2$ , we have $P_{22}^Ef=yz$ . Both projections eliminate $z^2$ . It is obvious by inspecting the matrix entries of the matrices of $\Gamma_E$ that $P_{12}^Ef$ and $P_{21}^Ef$ also eliminate $z^2$ . Since $z^2$ is not projected out of $f$ , it does not belong to $\Gamma_E$ . This implies that $f'=xz+yz$ transforms according to $\Gamma_E$ . In other words, any linear combination of a set of functions that transforms according to an irreducible representation of a point group is also a basis of the irreducible representation.

We can also define another projection operator, $P^q=\sum_{i=1}^{d_q}P_{ij}^q$ , where $j=i$ and $d_q$ is the dimension of $\Gamma_q$ . This projection operator employs the characters of an irreducible representation instead of matrix entries of every matrix representation, i.e.

$P^q=\sum_{i=1}^{d_q}P_{ii}^q=\frac{d_q}{\vert G\vert}\sum_{\alpha}^{\vert G\vert}\biggr\[\sum_{i=1}^{d_q}\Gamma_q^*(\alpha)_{ii}\biggr\]R_{\alpha}=\frac{d_q}{\vert G\vert}\sum_{\alpha}^{\vert G\vert}\chi_q^*(\alpha)R_{\alpha}\;\;\;\;\;\;\;\;94$

$\begin{matrix}if\;p\neq q&\;\;\;\;\;\;\;\;P^qf_l^p=0&\;\;\;\;\;\;\;\;96\\if\;p=q&\;\;\;\;\;\;\;\;P^qf_l^q=\sum_{i=1}^{d_q}\delta_{il}f_i^q=f_l^q&\;\;\;\;\;\;\;\;97\end{matrix}$

In contrast with $P_{il}^q$ (c.f. eq93), which projects $xz$ or $yz$ from $f'=xz+yz$ for $\Gamma_E$ , $P^q$ projects out the same basis function from $f'$ (easily shown using eq94). Since any linear combination of a set of basis functions of an irreducible representation of a point group is also a function that transforms according to the irreducible representation, we can express eq96 and eq97 as

$\begin{matrix}if\;p\neq q&\;\;\;\;\;\;\;\;P^qf_{com}^p=0&\;\;\;\;\;\;\;\;98\\if\;p=q&\;\;\;\;\;\;\;\;P^qf_{com}^q=f_{com}^q&\;\;\;\;\;\;\;\;99\end{matrix}$

where $f_{com}^v=\sum_{l=1}^{d_v}c_lf_l^v$ .

Finally, let’s examine the effect of a projection operator on a set of linearly independent basis functions $g_1,g_2,\cdots,g_s$ of an $s$ -dimensional reducible representation $\Gamma_R$ of a point group $G$ . Since $g_1,g_2,\cdots,g_s$ is a basis for $\Gamma_R$ , we have $R_{\alpha}g_j=\sum_{m=1}^sa_{mj}g_m$ or equivalently,

$\begin{pmatrix}R_{\alpha}g_1&R_{\alpha}g_2&\cdots &R_{\alpha}g_s\end{pmatrix}=\begin{pmatrix}g_1&g_2&\cdots &g_s\end{pmatrix}A$

where $A=\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1s}\\a_{21}&a_{22}&\cdots &a_{2s}\\\vdots&\vdots&\ddots &\vdots\\a_{s1}&a_{s2}&\cdots &a_{ss}\end{pmatrix}$ .

Let’s analyse the example for $s=3$ , where $A=\begin{pmatrix}a_{11}&a_{12} &a_{13}\\a_{21}&a_{22} &a_{23}\\a_{31}&a_{32} &a_{33}\end{pmatrix}$ and

$\begin{pmatrix}R_{\alpha}g_1&R_{\alpha}g_2 &R_{\alpha}g_3\end{pmatrix}=\begin{pmatrix}g_1&g_2 &g_3\end{pmatrix}A$

$A$ can undergo a similarity transformation to $A'$ , which has the block-diagonal form of:

$A'=\begin{pmatrix}a'_{11}&0 &0\\0&a'_{22} &a'_{23}\\0&a'_{32} &a'_{33}\end{pmatrix}\;\;\;\;\;\;\;\;100$

where each block is an irreducible representation.

It is obvious that $A'$ is a direct sum of irreducible representations of $G$ . The direct sum can also be obtained using eq27a. Let’s denote the basis functions of the transformed reducible representation by

$f_1^1,f_2^1,\cdots,f_{d_1}^1,f_1^2,f_2^2,\cdots,f_{d_2}^2,\cdots,f_1^k,f_2^k,\cdots,f_{d_k}^k$

where $d_k$ refers to the dimension of the $k$ -th irreducible representation of $G$ .

Therefore, we have

$\begin{pmatrix}R_{\alpha}f_1^1&R_{\alpha}f_1^2 &R_{\alpha}f_2^2\end{pmatrix}=\begin{pmatrix}f_1^1&f_1^2 &f_2^2\end{pmatrix}A'\;\;\;\;\;\;\;\;101$

Since a similarity transformation involves a change of basis, the old basis functions $g_s$ can be expressed as a linear combination of the new basis functions $f_{d_k}^k$ :

$g_s=\sum_{v=1}^k\sum_{i=1}^{d_v}c_{vi}^sf_i^v=\sum_{v=1}^kf_{s,com}^v\;\;\;\;\;\;\;\;102$

where $f_{s,com}^v=\sum_{i=1}^{d_v}c_{vi}^sf_i^v$ , i.e. $f_{s,com}^v$ also transforms according to the $v$ -th irreducible representation of $G$ .

Applying the projection operator to eq102 and using eq98 and eq99,

$P^qg_s=\sum_{v=1}^kP^qf_{s,com}^v=f_{s,com}^q\;\;\;\;\;\;\;\;103$

With reference to the LHS of eq103, $P^qg_s$ results in a linear combination of $g_s$ because $P^q$ is itself a linear combination of symmetry operators of $G$ (c.f. eq94). This linear combination of $g_s$ , according to the RHS of eq103, is equal to a function that transforms according to an irreducible representation $\Gamma_q$ of $G$ . Such a consequence is used to construct symmetry-adapted linear combination (SALC) of orbitals, which shall be discussed in the next article.

Projection operator (group theory)

Question

Answer

Next article: Symmetry-adapted linear combination (SALC) of orbitals

Previous article: Vanishing integrals

Content page of group theory

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply