A vanishing integral is a continuous sum of a function that evaluates to zero. Group theory allows us to identify a vanishing integral as a result of the symmetry of the system.
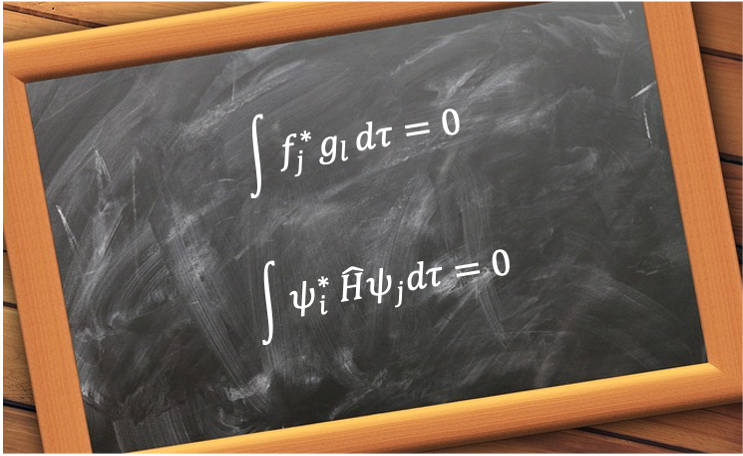
Consider a set of basis functions that transforms according to a representation
of a point group
. The integral of an element of the function
is a scalar, which is invariant to any symmetry operation
of the coordinate system, i.e.
Since there are number of symmetry operations of
, we can write
equations of eq82 and sum them to give
Let , where
and
belong to the sets of linearly independent functions
and
respectively, and where
and
are bases for the irreducible representations
and
respectively of
. Substituting
and eq77i in eq83,
Rewrite eq20 as and substitute it in eq84 to give
We conclude that:
|
Rule 1 |
If |
This implies that basis functions belonging to different non-equivalent irreducible representations are orthogonal. With respect to eq76 and eq77i, if transforms according to the totally symmetric representation of
and
transforms according to a different irreducible representation
of
, then
must transform according to
, which is obviously not the total symmetric representation of
. Therefore,
| Rule 2 | If a function transforms according to an irreducible representation that is not the totally symmetric representation of a group, its integral over all space is necessarily zero |
Next, we look at the quantum-mechanical integral , where
and
are wavefunctions and
is a quantum-mechanical operator, which is also a function.
Question
Why is an operator a function?
Answer
A function is a mapping of each element of the set
in one vector space of functions
to one element of the set
in another vector space of functions
, which may be the same space as
. Similarly, an operator maps each element (e.g. a wavefunction) of a vector space of functions
to another element in another vector space of functions
, which may be the same space as
.
Due to rule 1, is necessarily zero if
and
transform according to two different non-equivalent irreducible representations. Let’s consider the integral
, where
,
and
transform according to the irreducible representations
,
and
respectively of a group
. Since the non-relativistic Hamiltonian
is invariant under any symmetry operation, it transforms according to the totally symmetric irreducible representation of
. With reference to eq76 and eq77i,
consequently transforms according to
. Therefore,
if
.
Question
Do the integrals and
vanish in a
molecule?
Answer
is totally symmetric, while
and
transform according to two different non-equivalent irreducible representations
and
respectively. Therefore,
. Using eq76,
transforms according to
. Hence,
is not necessarily zero.
Finally, the evaluation of vanishing integrals often involves analysing functions that transform according to the direct sum of irreducible representations. For example,
Since integration is a linear operation, and the sum of two vectors in any vector space is given by the sum of their individual components, the integral of a matrix-valued function is the matrix consisting of the integrals of its individual components:
This linear integration process is useful in determining transition selection rules, which may involve functions that transform according to direct product representations that decompose into direct sums of irreducible representations (see this link for an example).
