The generating function for Hermite polynomials is a mathematical tool that, when expanded as a power series, yields the ratio of the Hermite polynomials
and the factorial of the summation index as its coefficients.
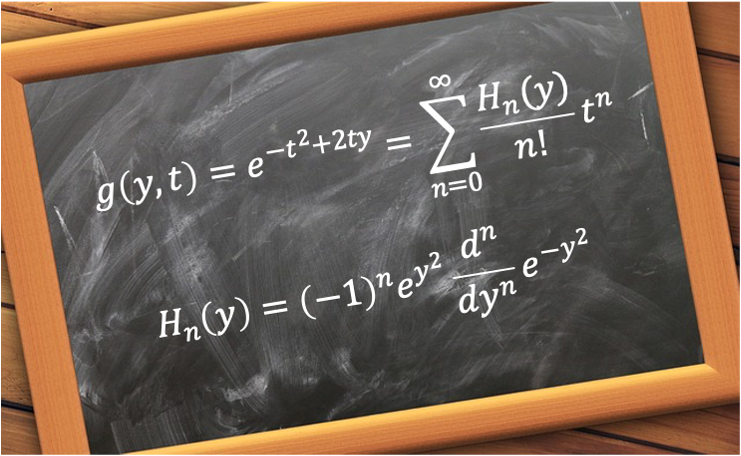
It can also be used to derive the normalisation constant for the wavefunctions of the quantum harmonic oscillator, and is defined as
To prove the 2nd equality of eq33, we take the partial derivative of with respect to
to give
. Substituting eq29 in this equation, we have
The solution to the differential equation is
When , eq34 becomes
Using eq19,
Using eq20,
Since the Maclaurin series expansion of is
, we have
, which completes the proof.
The generating function can be used to derive the Rodrigues formula for Hermite polynomials. From 33,
Let . We have
and
. Therefore,
Substitute eq36 in eq35
When
From eq33
Substitute eq39 into eq38
Eq40 is the Rodrigues formula for Hermite polynomials. In other words, the Rodrigues formula for Hermite polynomials is a mathematical expression that provides a method to calculate any Hermite polynomial using differentiation.
