Generating function and Rodrigues’ formula for the Hermite polynomials

The generating function $g(y,t)$ for Hermite polynomials is a mathematical tool that, when expanded as a power series, yields the ratio of the Hermite polynomials $H_n(y)$ and the factorial of the summation index as its coefficients.

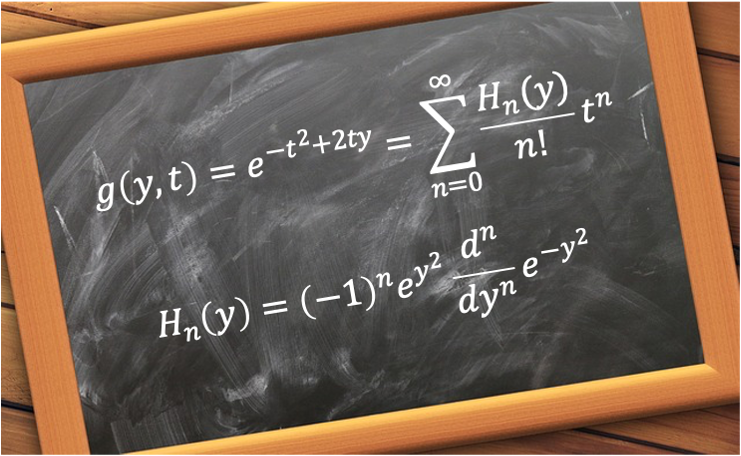
It can also be used to derive the normalisation constant for the wavefunctions of the quantum harmonic oscillator, and is defined as

$g(y,t)=e^{-t^2+2ty}=\sum_{n=0}^{\infty}\frac{H_n(y)}{n!}t^n=H_0(y)+H_1(y)t+\frac{1}{2!}H_2(y)t^2+\cdots\;\;\;\;\;\;\;\;33$

To prove the 2^nd equality of eq33, we take the partial derivative of $g$ with respect to $y$ to give ${\frac{\partial g(y,t)}{\partial y}=\sum_{n=0}^{\infty}\frac{dH_n(y)}{dy}\frac{t^n}{n!}}$ . Substituting eq29 in this equation, we have

${\frac{\partial g(y,t)}{\partial y}=\sum_{n=0}^{\infty}2nH_{n-1}(y)\frac{t^n}{n!}=2H_0(y)t+\frac{2(2)}{2!}H_1(y)t^2+\frac{2(3)}{3!}H_2(y)t^3+\cdots=2tg(y,t)}$

The solution to the differential equation ${\frac{\partial g(y,t)}{\partial y}-2tg(y,t)=0$ is

$g(y,t)=e^{2ty}f(t)\;\;\;\;\;\;\;\;34$

When $y=0$ , eq34 becomes

$g(0,t)=f(t)=\sum_{n=0}^{\infty}\frac{H_n(0)}{n!}t^n=H_0(0)+H_1(0)t+\frac{H_2(0)}{2!}t^2+\cdots$

Using eq19,

$f(t)=H_0(0)+\frac{H_2(0)}{2!}t^2+\frac{H_4(0)}{4!}t^4+\cdots=\sum_{n=0}^{\infty}\frac{H_{2n}(0)}{(2n)!}t^{2n}$

Using eq20,

$f(t)=\sum_{n=0}^{\infty}\frac{(-1)^n(2n)!}{(2n)!n!}t^{2n}=\sum_{n=0}^{\infty}\frac{(-1)^n}{n!}t^{2n}$

Since the Maclaurin series expansion of $e^x$ is ${\sum_{n=0}^{\infty}\frac{x^n}{n!}}$ , we have ${f(t)=\sum_{n=0}^{\infty}\frac{(-1)^n}{n!}t^{2n}=e^{-t^2}}$ , which completes the proof.

The generating function can be used to derive the Rodrigues formula for Hermite polynomials. From 33,

$g(y,t)=e^{-t^2+2ty}=e^{y^2-(t-y)^2}=e^{y^2}e^{-(t-y)^2}$

$\frac{\partial g(y,t)}{\partial t}=e^{y^2}\frac{\partial}{\partial t}e^{-(t-y)^2}\;\;\;\;\;\;\;\;35$

Let $f=e^{-(t-y)^2$ . We have ${\frac{\partial f}{\partial t}=-(2t-2y)e^{-(t-y)^2}}$ and ${\frac{\partial f}{\partial y}=(2t-2y)e^{-(t-y)^2}}$ . Therefore,

$\frac{\partial f}{\partial t}=-\frac{\partial f}{\partial y}\;\;\;\;\;\;\;\;36$

Substitute eq36 in eq35

$\frac{\partial g(y,t)}{\partial t}=e^{y^2}\frac{\partial}{\partial t}e^{-(t-y)^2}=(-1)e^{y^2}\frac{\partial}{\partial y}e^{-(t-y)^2}$

$\frac{\partial^n g(y,t)}{\partial t^n}=e^{y^2}\frac{\partial^n}{\partial t^n}e^{-(t-y)^2}=(-1)e^{y^2}\frac{\partial}{\partial y}\frac{\partial^{n-1}}{\partial t^{n-1}}e^{-(t-y)^2}=\\(-1)^ne^{y^2}\frac{\partial^n}{\partial y^n}e^{-(t-y)^2}\;\;\;\;\;\;\;n=1,2,\cdots\;\;\;\;\;\;\;\;37$

When $t=0$

$\frac{\partial^n g(y,t)}{\partial t^n}_{t=0}=(-1)^ne^{y^2}\frac{\partial^n}{\partial y^n}e^{-y^2}\;\;\;\;\;\;\;\;38$

From eq33

$\frac{\partial g(y,t)}{\partial t}=H_1(y)+H_2(y)t+\frac{1}{2}H_3(y)t^2+\frac{1}{6}H_4(y)t^3\cdots$

$\frac{\partial^2 g(y,t)}{\partial t^2}=H_2(y)+H_3(y)t+\frac{1}{2}H_4(y)t^2+\cdots$

$\frac{\partial^n g(y,t)}{\partial t^n}=H_n(y)+H_{n+1}(y)t+\frac{1}{2}H_{n+2}(y)t^2+\cdots$

$\frac{\partial^n g(y,t)}{\partial t^n}_{t=0}=H_n(y)\;\;\;\;\;\;\;\;39$

Substitute eq39 into eq38

$H_n(y)=(-1)^ne^{y^2}\frac{d^n}{dy^n}e^{-y^2}\;\;\;\;\;\;\;\;40$

Eq40 is the Rodrigues formula for Hermite polynomials. In other words, the Rodrigues formula for Hermite polynomials is a mathematical expression that provides a method to calculate any Hermite polynomial using differentiation.

Generating function and Rodrigues’ formula for the Hermite polynomials

Next article: Normalisation constant for the wavefunctions of the quantum harmonic oscillator

Previous article: Taylor series of single-variable and multi-variable functions

Content page of vibrational spectroscopy

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply