Group theory plays a pivotal role in understanding molecular symmetry and electronic properties in inorganic chemistry, particularly when applied to transition metal compounds.
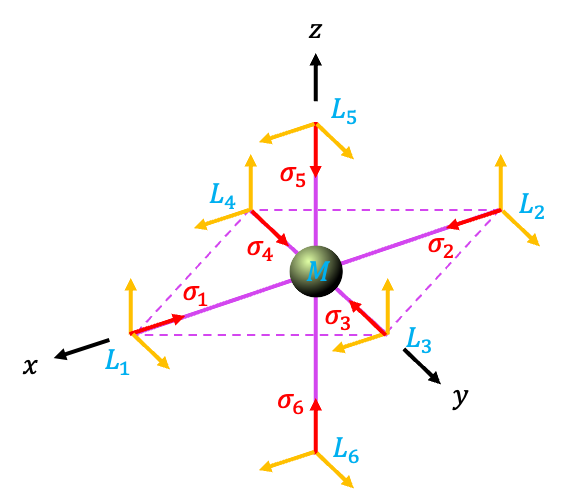
Sigma interactions
Consider an octahedral molecule (see diagram above), which belongs to the
point group. Let’s assume that valence atomic orbitals (AO) of the transition metal
participate in bonding with the valence orbitals of the ligands
, specifically
-orbitals with
symmetry. The wavefunctions of these ligand orbitals shall be denoted by
, where
. To generate a molecular orbital (MO) diagram for the complex, we need to perform the following steps:
-
- Find the symmetry of the AOs of
.
- Determine the symmetry of the symmetry-adapted linear combinations (SALC) of
.
- Work out which AOs of
have non-zero vanishing integrals with valence orbitals of
.
- Find the symmetry of the AOs of
For step 1, the central atom lies on all the planes and axes of symmetry of the
point group and is invariant to all symmetry operations
of the
point group. Therefore, the valence AOs of
must transform according to respective bases of the character table of the
point group.
| Valence |
Irreducible representations of |
To accomplish step 2, we need to
-
- Select a basis set to generate a reducible representation
of the
point group.
- Calculate the traces of the matrices of
.
- Decompose
into irreducible representations of the
point group.
- Generate a set of orthogonal SALCs.
- Select a basis set to generate a reducible representation
We shall employ the -vectors in the
diagram as a basis set. The direction of each vector indicated in the diagram is regarded as the positive lobe of the ligand
-orbital. Instead of carrying out the laborious task of letting
act on the basis set to produce matrices for the reducible representation, we can determine the traces by inspection. This is because each
-vector is transformed by
into another
-vector but not into a linear combination of
-vectors. Furthermore, a diagonal element of a matrix of
is equal to 1 when
leaves a
-vector invariant. For example, a
operation along the
-axis leaves
and
invariant, giving a trace of 2. The result is
| 6 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 4 | 2 |
Using eq27a, decomposes to
.
This implies that the matrices of are block-diagonal matrices of the same form. Each block-diagonal matrix is composed of the direct sum of the three irreducible representations
,
and
of the
point group. Since the number of basis functions of an irreducible representation corresponds to the dimension of the representation, there are a total of six such functions for
(one for
, two for
, and three for
).
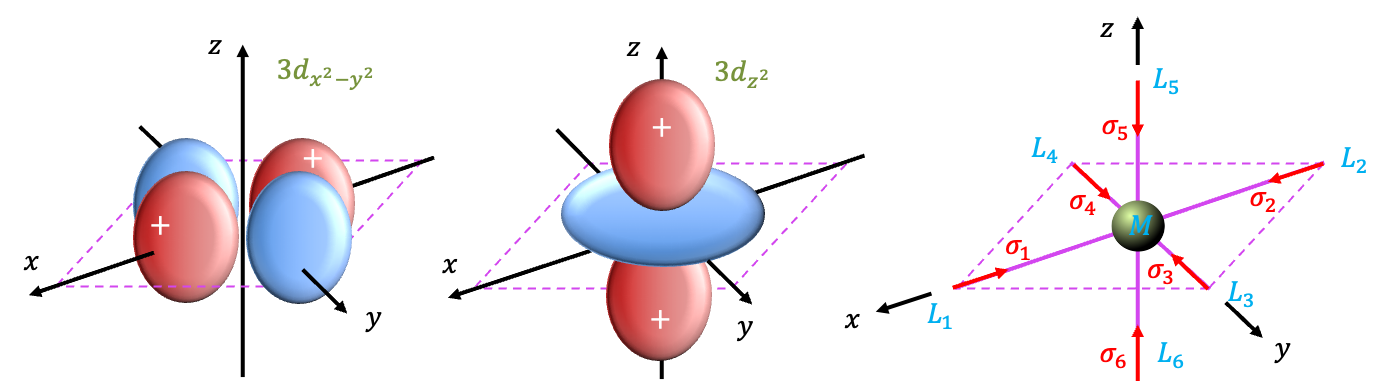
Instead of generating the basis functions, known as SALCs, using the projection operator, we shall derive them by logic. The SALC that transforms according to
must totally symmetric. This is only possible if
because the operation
simply permutates the order of
in
, i.e.
. There are three SALCs
,
and
that transform according to
. Since non-zero vanishing integrals occur only when they overlap with AOs of
belonging to
, these linear combinations must behave the same as the three
-orbitals of
under symmetry operations. By inspection, we find that
transforms like
of
,
transforms like
of
and
transforms like
of
. It follows that the two SALCs
and
that transform according to
have to behave the same as
and
of
under symmetry operations (see diagram above). Therefore,
because
has positive lobes along the
-axis and negative lobes along the
-axis. The last SALC is
and not
because the latter is not orthogonal to the other SALCs. Therefore, the normalised set of SALCs are:
To construct the MO diagram, we refer to eq157 of the Hartree-Fock-Roothaan method. The total wavefunction is , where
is the antisymmetriser and
and
represents the AOs of
and
in the SALCs. In general, a solution of eq157 for the
complex produces the following result:
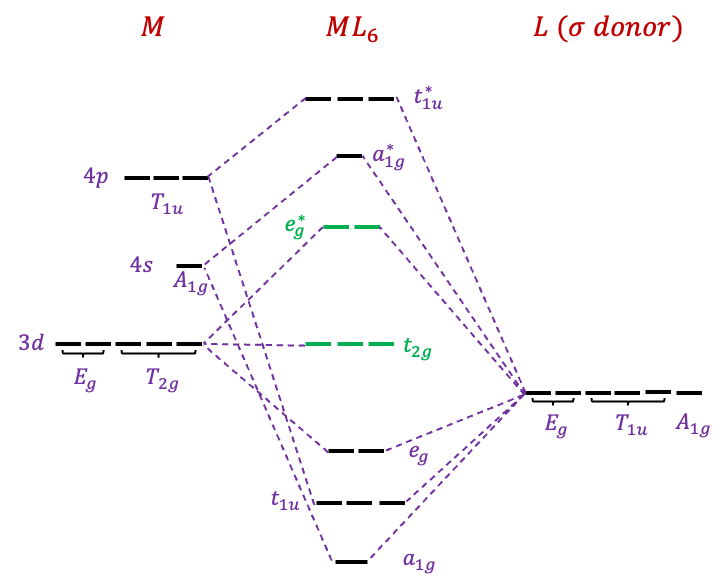
The lowest six MOs of ,
and
are bonding orbitals. They are occupied by 12 electrons, which are supplied by the six electron-donor ligands. The highest six MOs of
,
and
are antibonding orbitals. This leaves three MOs of
symmetry as non-bonding MOs. The valence
-electrons of
occupied the five MOs in green. The relative order of some of the MOs may vary depending on the types of metal and ligand.

Question
Do the remaining -orbitals (other than those of
symmetry) and the
-orbitals of the ligands participate in bonding with the valence AOs of
?
Answer
Yes, they may participate in bonding. When selected as a basis set, the six -orbtials of the ligands generate a reducible representation with matrices that have the same traces as those of
. The SALCs also matches the six SALCs derived above. It follows that the MO diagram, when both
-orbitals with
symmetry and
-orbitals participate in bonding with
, will be a superposition of two very similar MO diagrams.
The remaining -orbitals form
-bonds with the
orbitals of
. Such interactions will be discussed below.
Pi interactions
We shall utilise the remaining vectors in the diagram as a basis set. The direction of each vector indicated in the diagram is regarded as the positive lobe of the ligand
-orbital. Employing the same logic as we did for
interactions, we have
| 12 | 0 | 0 | 0 | -4 | 0 | 0 | 0 | 0 | 2 |
Using eq27a, is decomposes to
.
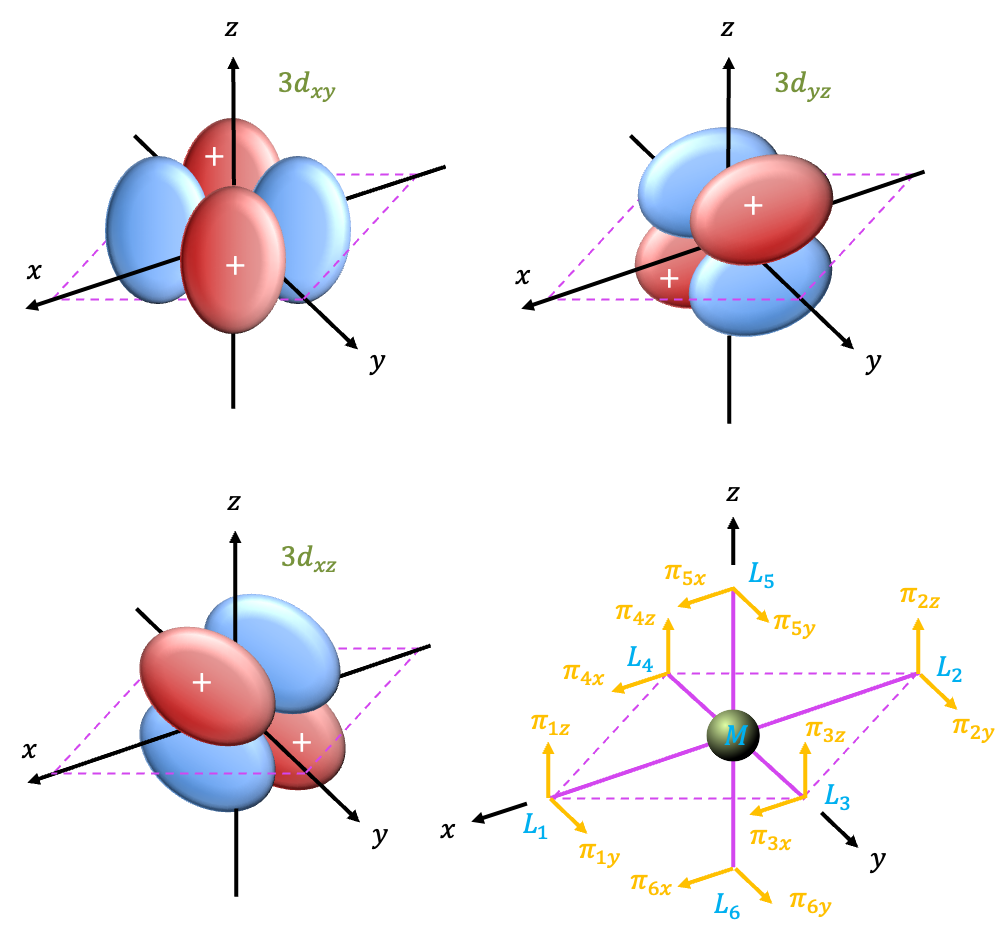
The orthonormal SALCs are
|
Irreducible representations |
Orthonormal ligand SALCs | Metal atom AOs |
| Non-bonding | Non-bonding | |
| Non-bonding | Non-bonding |
The MO diagram, which describes both sigma and pi interactions, has the following general form:
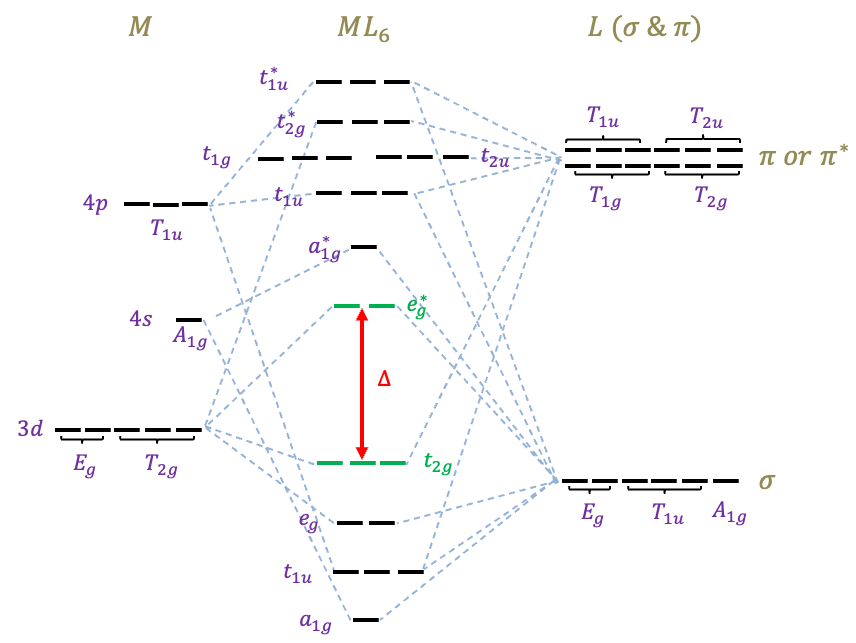
The and
MOs are non-bonding, while the
MOs are now bonding. The relative order of some of the MOs may vary depending on the type of complex and whether the ligands are
-acceptors or
-donors. For instance, the energies of the
MOs are usually lower than those of the
MOs for
-donors ligands. Examples of ligands that can engage in both sigma and pi interactions include
and
, while examples of
-acceptors and
-donors ligands are
and
, respectively. These MO diagrams provide the theoretical foundation for the ligand field theory.