The recurrence relations of the associated Laguerre polynomials describe how each polynomial in the sequence can be obtained from its predecessors.
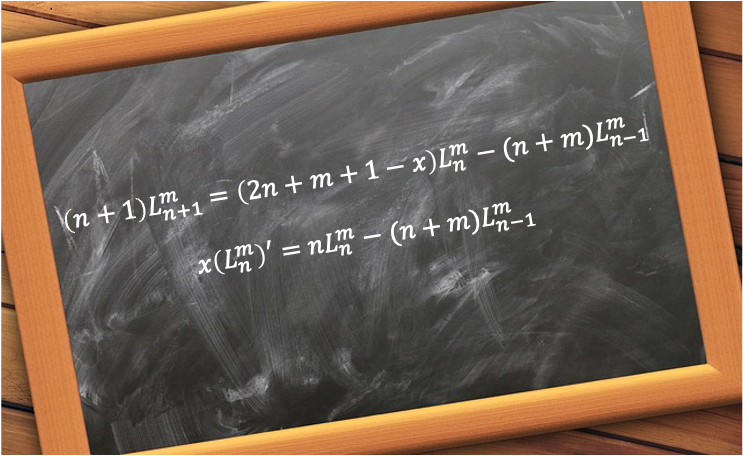
Some useful recurrence relations of the associated Laguerre polynomials include
Eq450 can be proven by differentiating the generating function for the associated Laguerre polynomials (see eq448) with respect to to give
Substituting eq448 yields
Equating the coefficients of and rearranging them results in eq450. Eq451 can be proven by replacing with
in the recurrence relations of the Laguerre polynomials (see eq436) to give
Differentiating this equation times with respect to
using Leibniz’ theorem and multiplying through by
yields
Only the last two terms in the summation ( and
) survives. Therefore,
Substituting eq443 and rearranging the result gives eq451.