The orthogonality of the associated Laguerre polynomials states that the integral of the product of two distinct associated Laguerre polynomials over a specified interval is zero.
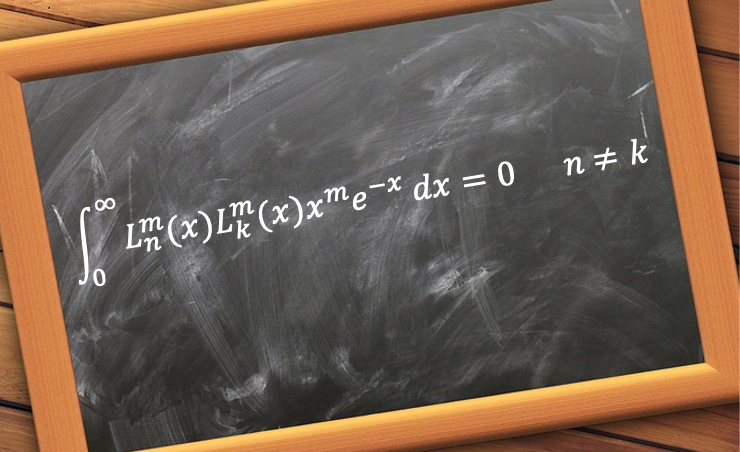
It is defined mathematically as:
where is known as a weight function.

Question
Why is the weight function included? Can the orthogonality of the associated Laguerre polynomials be defined as , where
? Why are the limits of integration from 0 to
? Why are the polynomials
and not
?
Answer
The weight function is an integral part of the orthogonality definition of associated Laguerre polynomials due to its role in ensuring convergence and its practical applications. It is often tied to specific problems, such as those in quantum mechanics. Omitting the weight function would sever this connection and could potentially alter the orthogonality properties of the polynomials. Therefore, defining orthogonality without the weight function would generally be invalid and would not reflect the intended use and properties of the associated Laguerre polynomials.
The weight function naturally defines the integration range because as
, making the integral convergent over this range. This range is also connected to specific problems, such as the radial part of the wave functions in quantum mechanics. In the context of the hydrogen atom,
represents a distance, which is always non-negative.
The eigenvalue of is a function of
and not
. Since the eigenfunctions of a Hermitian operator are orthogonal, two associated Laguerre polynomials with distinct values of
must be orthogonal. If we allow the values of
to be different, we wouldn’t know if the result of the integral is solely due to the values of
.
To prove eq453, we multiply the generating function for the associated Laguerre polynomials (see eq448) for and
to give
Multiplying through by and integrating with respect to
yields

Question
Show that , where
is a non-negative integer.,
Answer
Let ,
and
, and then
and
. Integrating by parts,
Let and
, and then
and
. Integrating by parts
If we carry out integrations by parts, we have
Therefore, eq454 becomes
Expressing the LHS as a binomial series,
So,
Equating the coefficients of when
gives eq453.