Orthogonality of the associated Laguerre polynomials

The orthogonality of the associated Laguerre polynomials states that the integral of the product of two distinct associated Laguerre polynomials over a specified interval is zero.

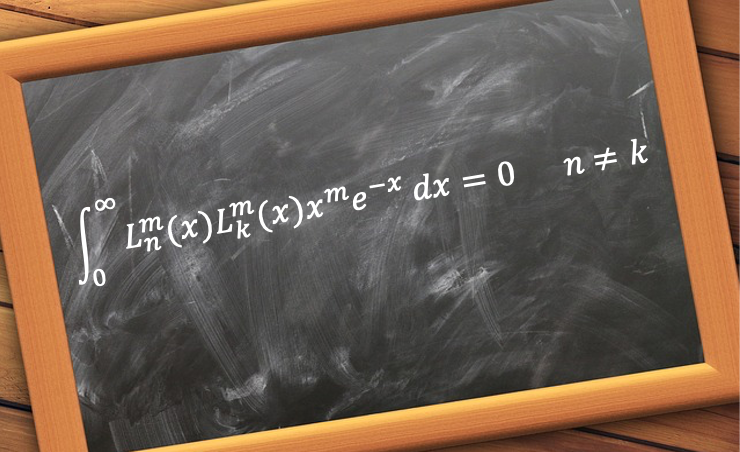
It is defined mathematically as:

$\int_0^{\infty}L_n^m(x)L_k^m(x)x^me^{-x}dx=0\;\;\;\;n\neq k\;\;\;\;\;453$

where $x^me^{-x}$ is known as a weight function.

Question

Why is the weight function included? Can the orthogonality of the associated Laguerre polynomials be defined as $\int_0^{\infty}L_n^m(x)L_k^m(x)dx=0$ , where $n\neq k$ ? Why are the limits of integration from 0 to $\infty$ ? Why are the polynomials $L_n^m(x)L_k^m(x)$ and not $L_n^m(x)L_k^r(x)$ ?

Answer

The weight function is an integral part of the orthogonality definition of associated Laguerre polynomials due to its role in ensuring convergence and its practical applications. It is often tied to specific problems, such as those in quantum mechanics. Omitting the weight function would sever this connection and could potentially alter the orthogonality properties of the polynomials. Therefore, defining orthogonality without the weight function would generally be invalid and would not reflect the intended use and properties of the associated Laguerre polynomials.

The weight function naturally defines the integration range because $x^me^{-x}\rightarrow 0$ as $x\rightarrow\infty$ , making the integral convergent over this range. This range is also connected to specific problems, such as the radial part of the wave functions in quantum mechanics. In the context of the hydrogen atom, $x$ represents a distance, which is always non-negative.

The eigenvalue of $L_n^m(x)$ is a function of $n$ and not $m$ . Since the eigenfunctions of a Hermitian operator are orthogonal, two associated Laguerre polynomials with distinct values of $n$ must be orthogonal. If we allow the values of $m$ to be different, we wouldn’t know if the result of the integral is solely due to the values of $n$ .

To prove eq453, we multiply the generating function for the associated Laguerre polynomials (see eq448) for $L_n^m(x)$ and $L_k^m(x)$ to give

$\frac{e^{-\frac{xt}{1-t}-\frac{xs}{1-s}}}{(1-t)^{m+1}(1-s)^{m+1}}=\sum_{n=0}^{\infty}\sum_{k=0}^{\infty}L_n^m(x)L_k^m(x)t^ns^k$

Multiplying through by $x^me^{-x}$ and integrating with respect to $x$ yields

$\int_0^{\infty}\frac{x^me^{-\[\frac{1-st}{(1-t)(1-s)}\]x}}{(1-t)^{m+1}(1-s)^{m+1}}dx=\sum_{n=0}^{\infty}\sum_{k=0}^{\infty}\biggr\{\int_0^{\infty}x^me^{-x}L_n^m(x)L_k^m(x)dx\biggr\}t^ns^k\;\;\;\;\;\;\;\;454$

Question

Show that $\int_0^{\infty}x^me^{-ax}dx=\frac{m!}{a^{m+1}}$ , where $m$ is a non-negative integer.,

Answer

Let $I_m=\int_0^{\infty}x^me^{-ax}dx$ , $u=x^m$ and $dv=e^{-ax}dx$ , and then $du=mx^{m-1}dx$ and $v=-\frac{1}{a}e^{-ax}$ . Integrating by parts,

$I_m=\biggr\[-\frac{x^me^{-ax}}{a}\biggr\]_0^{\infty}+\frac{m}{a}\int_0^{\infty}x^{m-1}e^{-ax}dx=\frac{m}{a}I_{m-1}$

Let $u=x^{m-1}$ and $dv=e^{-ax}dx$ , and then $du=(m-1)x^{m-2}dx$ and $v=-\frac{1}{a}e^{-ax}$ . Integrating by parts

$I_{m-1}=\biggr\[-\frac{x^{m-1}e^{-ax}}{a}\biggr\]_0^{\infty}+\frac{m-1}{a}\int_0^{\infty}x^{m-2}e^{-ax}dx=\frac{m-1}{a}I_{m-2}$

If we carry out $m$ integrations by parts, we have

$\begin{align}I_{m} &=\frac{m}{a}I_{m-1}=\frac{m(m-1)}{a^2}I_{m-2}=\cdots=\frac{m(m-1)\cdots(m-m+1)}{a^m}I_{0}\\&=\frac{m!}{a^m}\int_0^{\infty}e^{-ax}dx=\frac{m!}{a^m}\biggr\[-\frac{e^{-ax}}{a}\biggr\]_0^{\infty}=\frac{m!}{a^{m+1}}\end{align}$

Therefore, eq454 becomes

$\frac{m!}{(1-st)^{m+1}}=\sum_{n=0}^{\infty}\sum_{k=0}^{\infty}\biggr\{\int_0^{\infty}x^me^{-x}L_n^m(x)L_k^m(x)dx\biggr\}t^ns^k$

Expressing the LHS as a binomial series,

$\begin{align}m!(1-st)^{-(m+1)} &=m!\sum_{k=0}^{\infty}\begin{pmatrix}-m-1\\k\end{pmatrix}(-st)^k=m!\sum_{k=0}^{\infty}(-1)^k\frac{(-m-1)!}{k!(-m-1-k)!}(st)^k\\&=m!\sum_{k=0}^{\infty}(-1)^k\frac{(-m-1)(-m-2)\cdots(-m-k)}{k!}(st)^k\\&=m!\sum_{k=0}^{\infty}\frac{(m+1)(m+2)\cdots(m+k)}{k!}(st)^k\\&=m!\sum_{k=0}^{\infty}\frac{(m+k)!}{k!m!}(st)^k=\sum_{k=0}^{\infty}\frac{(m+k)!}{k!}(st)^k\end{align}$

So,

$\sum_{k=0}^{\infty}\frac{(m+k)!}{k!}(st)^k=\sum_{n=0}^{\infty}\sum_{k=0}^{\infty}\biggr\{\int_0^{\infty}x^me^{-x}L_n^m(x)L_k^m(x)dx\biggr\}t^ns^k\;\;\;\;\;\;\;\;455$

Equating the coefficients of $t^ns^k$ when $n\neq k$ gives eq453.

Orthogonality of the associated Laguerre polynomials

Question

Answer

Question

Answer

Next article: Normalisation constant of the associated Laguerre polynomials

Previous article: REcurrence relations of the associated Laguerre polynomials

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply