The total wavefunction of a hydrogenic atom characterises the probability of locating an electron around the nucleus by incorporating both radial and angular components.
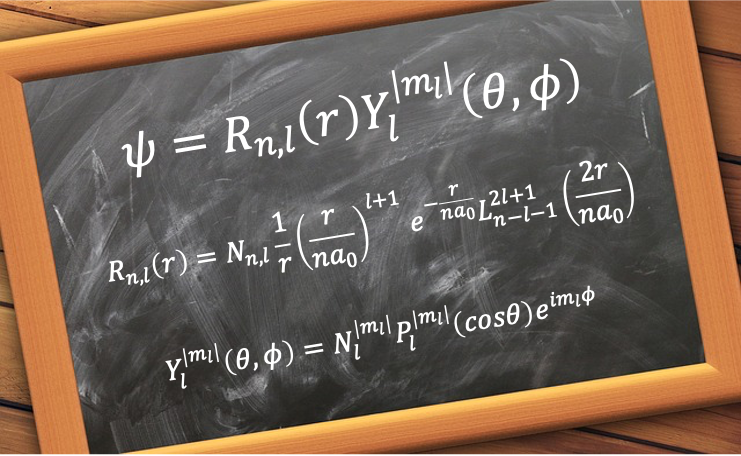
This spatial wavefunction is mathematically defined as:
where
, the radial wavefunction, is the radial component of
.
, the spherical harmonics, is the angular component of
.
are the associated Laguerre polynomials.
are the associated Legendre polynomials.
is the normalisation constant of the radial wavefunction.
is the normalisation constant of the spherical harmonics.
is the principal quantum number, where
is the orbital angular momentum quantum number (also known as azimuthal quantum number), where
and
.
is the magnetic quantum number, where
.
is the distance between an electron and the nucleus of a hydrogenic atom.
is the polar angle.
is the azimuthal angle.
is the Bohr radius.
is the reduced mass of the atom.
is the ratio of the Planck constant and
.
is the atomic number of the atom.
is the vacuum permittivity.