The vector model of quantum angular momentum

The vector model of angular momentum is a diagrammatic representation of the implications of the commutation relation of $\small \hat{L}^{2}$ with any one of the 3 component angular momentum operators.

In a previous article, we showed that it is possible to simultaneously specify eigenvalues of $\small \hat{L}^{2}$ and $\small \hat{L}_z$ because the 2 operators commute. Diagram I depicts the eigenvalues of $\small \hat{L}$ (i.e. the square root of eigenvalues of $\small \hat{L}^{2}$ ) and $\small \hat{L}_z$ .

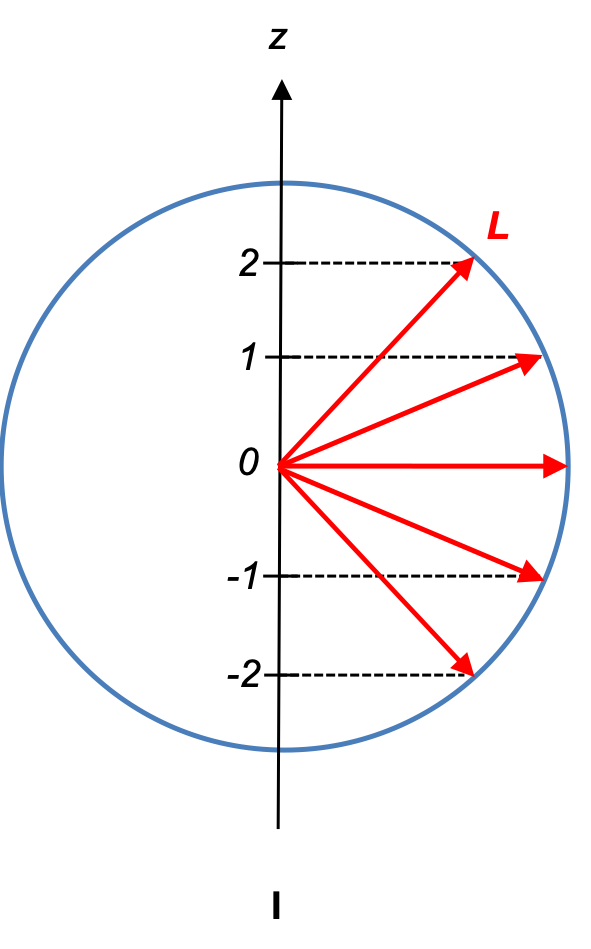
where axes are in $\small \hbar$ units; $\small \boldsymbol{\mathit{L}}$ is the angular momentum vector with magnitude $\small \sqrt{l(l+1)}$ , and has a $\small z$ -component of magnitude $\small m_l\in \mathbb{Z}$ .

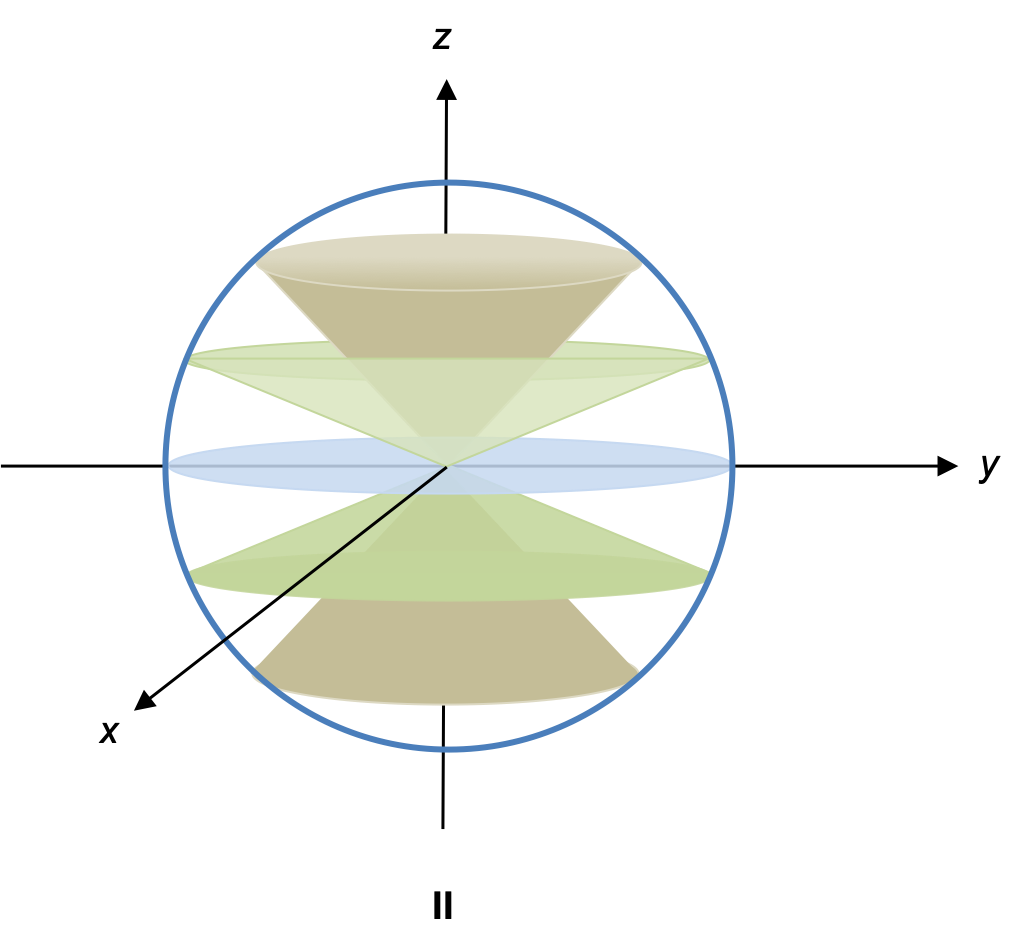
Since any one of the component angular momenta does not commute with any of the other two, we cannot simultaneously specify more than one component of angular momentum (other than the trivial case of $\small l_x=l_y=l_z=0$ ). The angular momentum vector therefore lies on the cones in diagram II at any azimuthal angle.

Question

Can $\small \boldsymbol{\mathit{L}}$ lie on the $\small z$ -axis?

Answer

No. If $\small \boldsymbol{\mathit{L}}$ lies on the $\small z$ -axis, $\small l_z$ is some non-zero integer while $\small l_x=l_y=0$ . This means we have specified all 3 angular momentum components, which is impossible.

The vector model of quantum angular momentum

Question

Next article: LArmor precession of an electron

Previous article: matrix elements of angular momentum ladder operators

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply