The structure factor, F, is a function that expresses the sum of amplitudes of scattered X-rays from all atoms in a crystal.
We have, in the previous section, discussed the scattering factor of a single atom, which is the sum of amplitudes of waves scattered by the electrons in the atom. We shall now describe the sum of amplitudes of scattered X-rays from all atoms in a unit cell.

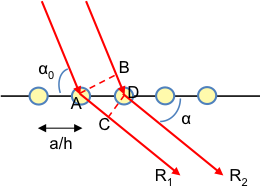
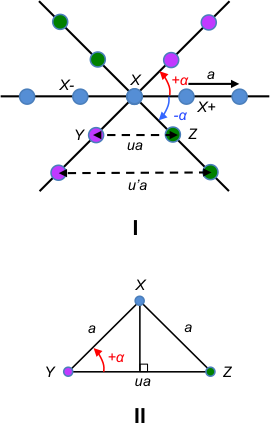
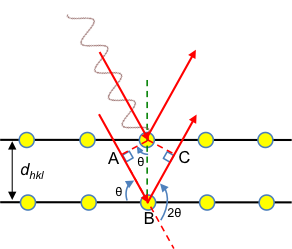
Consider a one-dimensional lattice along the a-axis consisting of two types of atoms (see diagram above). If the Laue equation along the a-axis is satisfied for R1 and R3 as well as for R2 and R4, we have:
However, if the Laue equation along the -axis is not satisfied for R1 and R2 (or for R2 and R3) we have:
Combining the two equations above and letting n = 1,
Substitute eq28 in eq34,
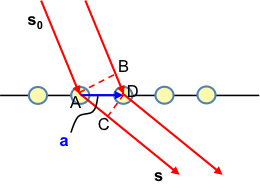
Recall from the previous section that the amplitude of the scattered X-ray received by the detector from an atom is equivalent to the scattering factor . If we have two atoms, the resultant amplitude F at the detector is
The second term in eq36 includes the factor eiΦ as the scattered rays from the second atom may have a phase difference from that from the first atom. If Φ = 0, F = f1+ f2 .

Question
Show that the intensity detected from eq36 is consistent with the intensity associated to the resultant amplitude of two general complex waves having a phase difference of Φ.
Answer
Let the waves be y1 = Aei(kx-ωt) and y2 = Bei(kx-ωt+Φ) . The resultant amplitude is y = Aei(kx-ωt) + y2 = Bei(kx-ωt+Φ). As we know, the intensity of the resultant wave is proportional to the square of magnitude of the amplitude of the wave:
Since
Similarly, for eq36
Substitute eq35 in eq36,
In three dimensions, eq37 becomes
So,
The first term in eq38 is in one-dimension. Since there is no phase difference between the resultant X-ray of the first atom with itself,
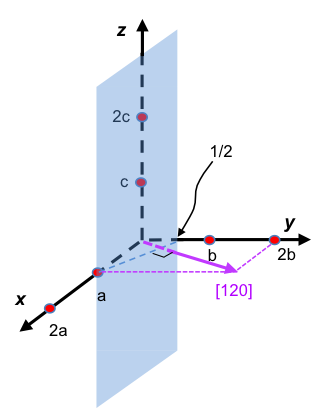
and eq38 is consistent with eq37, i.e. the phases of scattered X-rays of atoms are relative to that of the first atom at the coordinate of x1 = 0. Eq38 can be rewritten in terms of fractional coordinates:
where (i.e. xj in units of a),
,
.
The intensity of a diffraction signal is proportional to the square of the magnitude of the three-dimensional structure factor, i.e. and therefore systematic absences appear when
.
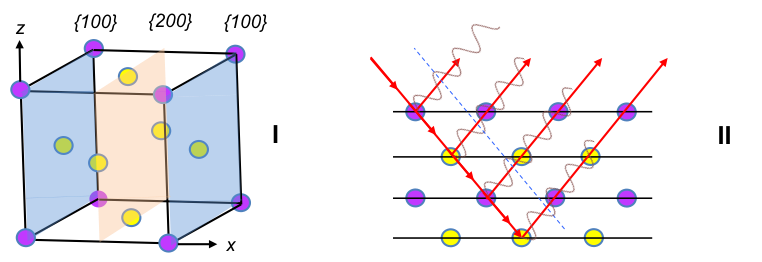
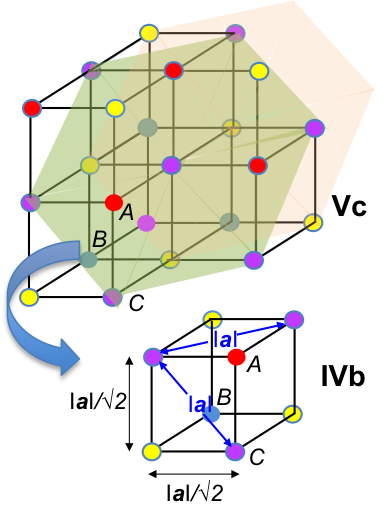
For example, the body centred cubic unit cell (where a = b = c) has fractional coordinates shown in the diagram below.

As the unit cell is composed of the same atoms, the structure factor for each atom is the same. If an atom is shared by m neighbouring unit cells, we multiply the scattering factor of the atom with 1/m. Therefore, eq39 becomes:
Since ei2π = cos2π + isin2π = 1, eiπ = cosπ + isinπ = -1 and eab = (ea)b
Since 1a = 1
If h + k + l is even, Fhkl = 2f. If h + k + l is odd, Fhkl = 0. Hence, systematic absences occur when h + k + l is odd. A primitive cubic unit cell is different from a BCC in that it does not have an atom at . Its structure factor is Fhkl = f, which means the diffraction intensities of a cubic P cell has no restriction other than the scattering factor of the atom, which is dependent on the Bragg’s angle θ and hence Bragg’s law of
.
For a face-centred cubic unit cell, the coordinates of the atoms are the same as a cubic P unit cell plus six other atoms on the six faces: ,
,
,
,
,
. These atoms are each shared by two neighbouring cells. The structure factor of a face-centred cubic unit cell is:
If h, k, l are all even or all odd, Fhkl = 4f. If one index is odd and two are even, or vice versa, Fhkl = 0. Therefore, a face-centred cubic unit cell does not have systematic absences when h, k, l are all even or all odd.