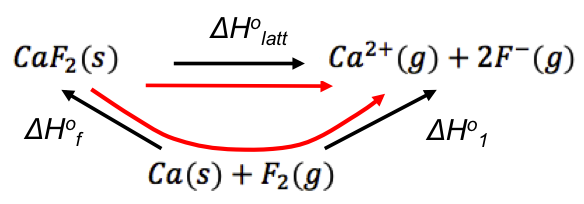Category: Intermediate Chemistry

The standard enthalpy change of electron gain, ΔH_eg^o, is the change in enthalpy when one mole of electrons is attached to atoms or anions in the gaseous state to form one mole of anions under standard conditions.

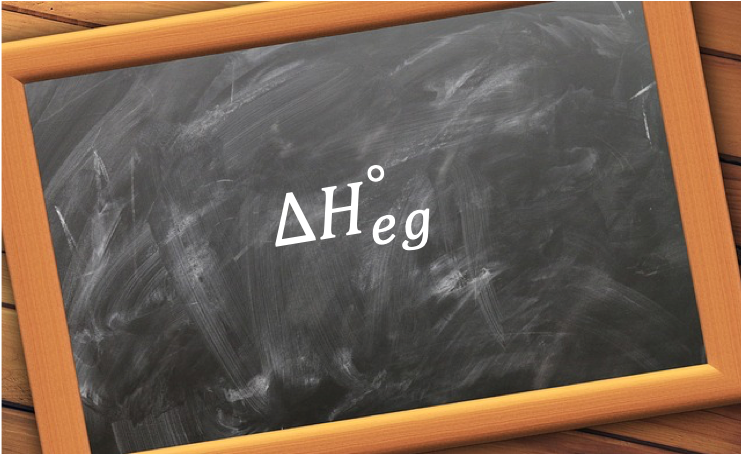
When one mole of electrons is attached to atoms to form one mole of monovalent anions, the change in enthalpy is called the first electron gain enthalpy, e.g.

When one mole of electrons is attached to monovalent anions to form one mole of divalent anions, the change in enthalpy is called the second electron gain enthalpy, e.g.

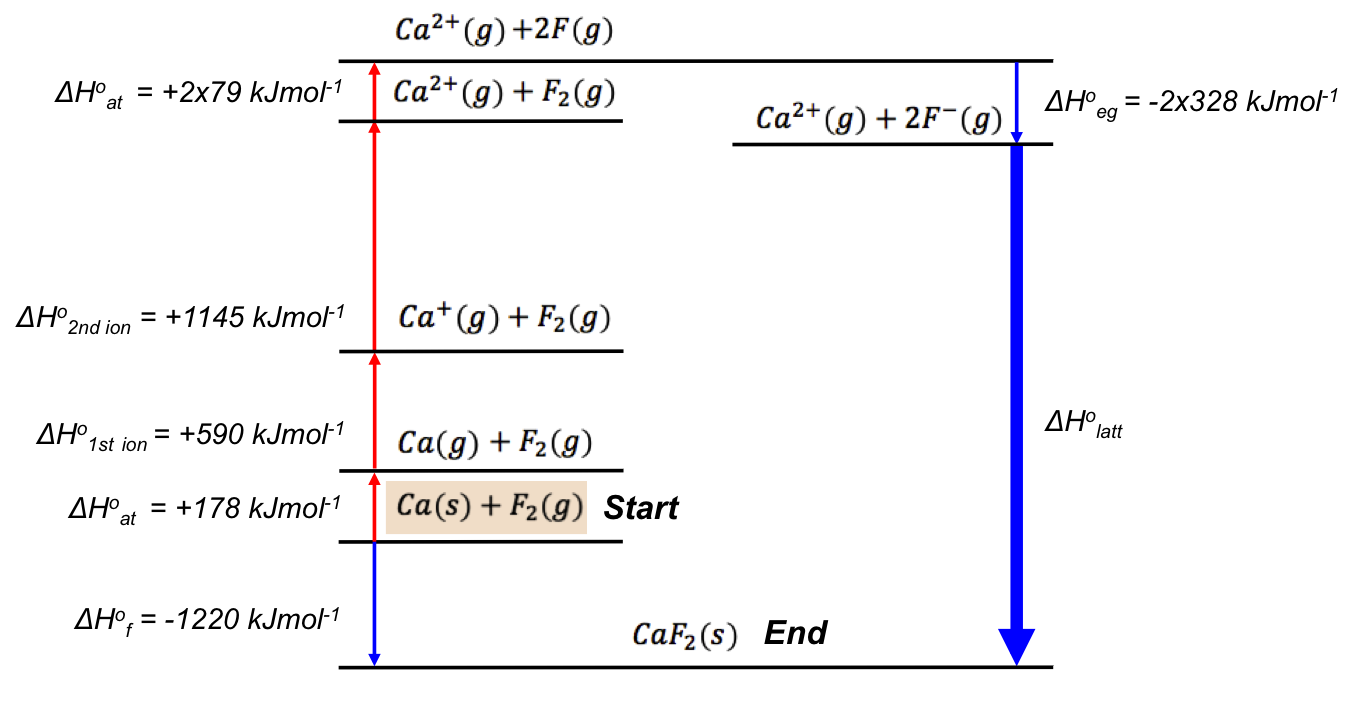
The standard enthalpy change of electron gain of a substance is calculated from the substance’s electron affinity (the two are not the same, as electron affinity is defined at absolute zero) using Kirchhoff’s law, or from the relationship:

which states that the standard enthalpy change of electron gain of a species is the negative of the standard enthalpy change of ionisation of that species with an additional electron attached, e.g.

Substituting eq3 from the previous section in eq5,

Electron affinities are determined experimentally using photoelectron spectroscopy (PES) where the known energy of an incident photon on an anion equals to the atom’s electron affinity plus the measured kinetic energy of the ionised electron. These electron affinities are then converted to electron affinities at absolute zero, which are then converted to standard enthalpies of electron gain, with both conversions using Kirchhoff’s law. It is easier to measure ionisation energies than electron affinities and therefore standard enthalpies of electron gain of substances are usually calculated using eq4.

 

Next article: Standard enthalpy change of hydration

Previous article: Standard enthalpy change of ionisation

Content page of intermediate chemical energetics

Content page of intermediate chemistry

Main content page

The standard enthalpy change of hydration, ΔH_hyd^o, is the change in enthalpy when one mole of an ion in the gaseous state dissolves in water to form an infinitely dilute solution under standard conditions. This means that we need to dissolve the solute in excess water until there is no change in the energy absorbed or released by the system.

Some examples are:

The standard enthalpy of hydration is always exothermic (negative) and increases (more negative) for ions with higher charge densities, i.e. higher charge-to-radius ratios.

 

Next article: Standard enthalpy change of solution

Previous article: Standard enthalpy change of electron gain

Content page of intermediate chemical energetics

Content page of intermediate chemistry

Main content page

The standard enthalpy change of solution, ΔH_sol^o, is the change in enthalpy when one mole of a solute dissolves in a solvent to form an infinitely dilute solution under standard conditions. This means that we need to dissolve the solute in excess solvent until there is no change in the energy absorbed or released by the system.

Some examples are:

Since KOH(aq) and HCl(aq) are fully dissociated in water, we can also write the above equation as:

ΔH_sol^o can be positive or negative. Compounds with large positive ΔH_sol^o are relatively insoluble.

 

Next article: Standard enthalpy change of lattice energy

Previous article: Standard enthalpy change of hydration

Content page of intermediate chemical energetics

Content page of intermediate chemistry

Main content page

The standard enthalpy change of neutralisation, ΔH_n ^o, is the change in enthalpy when one mole of water is formed from an acid reacting with an alkali, both in their most stable forms, under standard conditions.

For example,

or in the ionic form,

Since acids and alkalis, by definition, are in the aqueous state, their most stable form is the aqueous form. The standard enthalpy change of neutralisation in the above example is also the standard enthalpy change of reaction between sulphuric acid and sodium hydroxide to give sodium sulphate and water, i.e., ΔH_n ^o =ΔH_r ^o.

 

 

 

Next article: Standard enthalpy change of atomisation

Previous article: Standard enthalpy change of combustion

Content page of intermediate chemical energetics

Content page of intermediate chemistry

Main content page

The standard enthalpy change of lattice energy, ΔH_latt^o, is the change in enthalpy for breaking the bonds in one mole of a solid ionic compound and separating its gaseous ions to an infinite distance under standard conditions.

Since a large amount of energy is required to carry out the process, the standard enthalpy change of lattice energy of a compound is always positive (endothermic), e.g.

However, it may be defined as the change in enthalpy when one mole of an ionic solid is formed from its gaseous ions that are initially infinitely apart under standard conditions. If so, it will always be a negative value (exothermic).

The magnitude of the standard enthalpy change of lattice energy increases for ions with higher charge densities, leading to stronger electrostatic forces of attraction between them in the ionic lattice. Hence,

The standard enthalpy change of lattice energy of an ionic compound is determined theoretically using a Born-Haber cycle, as it is very hard to measure it precisely through experiments.

 

Next article: Other Standard enthalpy changes

Previous article: Standard enthalpy change of solution

Content page of intermediate chemical energetics

Content page of intermediate chemistry

Main content page

There are possibly as many standard enthalpy changes as there are types of reactions. Some common ones other than those mentioned in previous articles include:

1. 1. Standard enthalpy of hydrating an anhydrous salt (not to be confused with standard enthalpy of hydration), e.g.

1. 2. Standard enthalpy of precipitation, e.g.

 

 

Next article: Hess’s law

Previous article: Standard enthalpy change of lattice energy

Content page of intermediate chemical energetics

Content page of intermediate chemistry

Main content page

Hess’s law is named after Germain Hess, a Russian chemist, who published it in 1840. It is based on the principle of conservation of energy, and states that:

The total enthalpy change in a chemical reaction is sum of enthalpy changes of all steps from the reactants to the products regardless of the route taken.

For example, there are two possible chemical routes (indicated by red arrows in the diagram below) for the combustion of methane to form carbon dioxide and water:

On closer scrutiny, ΔH₁^o is composed of the following standard enthalpy changes of formation:

Similarly, ΔH₂^o is composed of the following standard enthalpy changes of formation:

The choice of the indices R and P will be apparent shortly. Hence,

where v_R and v_P are the stoichiometric coefficients of the products of the respective standard enthalpy change of formation reactions.

In general, for a reaction:

where R denotes the reactants and P denotes the products. Hess’ law states that:

Eq 6 is a very useful formula for calculating standard enthalpy changes.

 

 

 

Next article: Born-Haber cycle

Previous article: Other Standard enthalpy changes

Content page of intermediate chemical energetics

Content page of intermediate chemistry

Main content page

The Born-Haber cycle is a method to analyse reaction enthalpies, particularly to calculate the standard enthalpy change of lattice energy, ΔH_latt^o, which cannot be measured precisely via experiments. It is based on Hess’ law and was developed by the German scientists Max Born and Fritz Haber in 1916.

Born-Haber cycles are best represented in the form of energy diagrams. For example, if we want to calculate the standard enthalpy change of lattice energy of calcium fluoride, we start by writing the equations for ΔH_latt^o[CaF₂(s)] and ΔH_f^o[CaF₂(s)] :

Applying Hess’ law, we can combine the two equations into a cycle:

ΔH₁^o is composed of a few standard enthalpy changes. If we rewrite the cycle to include every standard enthalpy change (starting with the reactants of ΔH_f^o), we have the Born-Haber cycle for CaF₂(s):

The Born-Haber cycle (also known as the Born-Haber energy diagram) reveals that ΔH₁^o is composed of ΔH^o_at, ΔH^o_{1st ion}, ΔH^o_{2nd ion}, another ΔH^o_at and ΔH^o_eg. It is also evident that the sum of the magnitudes of each enthalpy on the left-hand side of the energy diagram is equal to that on the right-hand side, i.e.

The above computation shows that ΔH^o_latt for CaF₂ can be +2635 kJmol^-1 or -2635 kJmol^-1, depending on its definition. Since we have defined the standard enthalpy change of lattice energy as an endothermic process (see eq7, where ΔH^o_latt is the change in enthalpy to break the bonds in one mole of a solid ionic compound and separate its gaseous ions to an infinite distance under standard conditions),  ΔH_latt^o = +2635 kJmol^-1.

In summary, the steps involved in generating the Born-Haber cycle are:

1. 1. Write the equations for the standard enthalpy change of lattice energy and the standard enthalpy change of formation of the ionic compound.
   2. Combine the two equations into a cycle using Hess’ law.
   3. Expand the cycle in a stepwise manner to include every standard enthalpy change.
   4. Draw the Born-Haber cycle energy diagram starting with the reactants of the standard enthalpy change of formation of the compound and ending with the ionic compound.
   5. Sum the magnitude of enthalpies on each side of the cycle and equate them to find ΔH_latt^o.

Previous article: Hess’s law

Content page of intermediate chemical energetics

Content page of intermediate chemistry

Main content page

Cell notation is a shorthand representation of an electrochemical cell.

For example, the electrochemical cell depicted in the diagram above has a cell notation of

A vertical line represents a phase boundary, while a double vertical line signifies a phase boundary with negligible junction potential, such as a salt bridge. The anode half-cell is denoted on the left and the cathode half-cell on the right, with the electrodes (Pt and Cu) positioned at both ends of the notation.

A gas is always written adjacent to the electrode. Furthermore, spectator ions are usually omitted and state symbols and concentrations may be included for emphasis, e.g.

If the standard hydrogen electrode is undergoing reduction, its cell notation is:

 

 

Next article: Effects of concentration on E^o and the Nernst equation

Previous ARTICLE: Analysing reactions using standard electrode potentials

Content page of intermediate electrochemistry

Content page of intermediate chemistry

Main content page

Other than the standard hydrogen electrode (SHE), two other standard or reference electrodes are widely used: the calomel electrode and the silver chloride electrode. Each of these electrodes, like the SHE, provides a constant potential that is insensitive to the electrolyte.

Silver chloride electrode

The silver chloride reference electrode consists of a AgCl coated silver wire dipped in a saturated KCl solution (also saturated with AgCl). The porous frit, which allows for the slow passage of ions, forms a liquid junction with the test solution. The electrode potential of 0.199 V versus SHE at rtp is given by the following half-cell reaction:

Just as the constant bubbling of H₂ in a H⁺ (1 M) electrolyte of the SHE half-cell provides the electrode with a constant potential,  the Ag wire and the equilibrium between AgCl coated on the wire and the saturated AgCl internal solution ensure that the AgCl electrode maintains a constant potential. Some literature quotes the potential vs SHE as 0.22 V at rtp. This value corresponds to a KCl concentration of 1.0 M, whereas 0.199 V is measured when KCl is saturated.

The calomel electrode

The calomel reference electrode consists of mercury in contact with a saturated solution of Hg₂Cl₂ (calomel), which is in turn in contact with saturated KCl. The electrode potential of 0.244 V versus SHE at rtp is given by the following half-cell reaction:

Both AgCl and calomel reference electrodes are used for a wide range of electrochemical measurements. However, the toxicity of mercury in the calomel electrode poses health and environmental issues.

next article: standard electrode potentials

Previous article: standard hydrogen electrode

Content page of intermediate electrochemistry

Content page of intermediate chemistry

Main content page