What is formula describing the buffer capacity of an aqueous monoprotic weak acid and its conjugate base?
Consider a solution containing water, a strong base and a weak acid, HA, with the following equilibria:
With reference to the above equilibria, the sum of the number of moles of H+ and Na+ must equal to that of OH– and A– (see this article for details). As the volume is of the solution is common to all ions,
Substituting cb = [Na+] and Kw = [H+][OH–] in the above equation
Multiply the term [A–] on the RHS of the above equation by and noting that
, we have
where [HA]T =[HA] + [A–].
Substitute eq1 and pH = –log[H+] in the above equation
Substitute eq4a in the above equation
Comparing eq8 with eq7 with βs = 0 (since we are considering the case where a strong base is added to a solution containing water and a weak acid)
Since Ka is a constant
To determine the maximum or minimum buffer capacity of the weak monoprotic acid buffer,
Let
A stationary point for the function in eq10 occurs when Ka = [H+]. Since
Let’s investigate the nature of this stationary point by differentiating eq11.
Substitute eq13 in the above equation
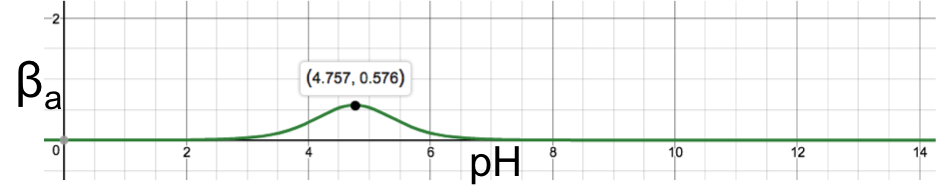
If we consider the case of the addition of a strong acid to the aqueous solution, we end up with the same conclusion. Hence, a monoprotic weak acid has maximum buffer capacity when [HA] = [A–]. The buffer capacity of the monoprotic weak acid over the entire range of pH can be found by substituting [H+] = 10-pH in eq10 to give
and plotting the above equation with βa as the vertical axis and pH as the horizontal axis to give:
The total buffer capacity of an aqueous monoprotic weak acid is given by the combined equations of eq8 and eq9, i.e.
The total buffer capacity of an aqueous monoprotic weak acid over the entire range of pH can be found by substituting eq6a and eq14 in eq15 to give
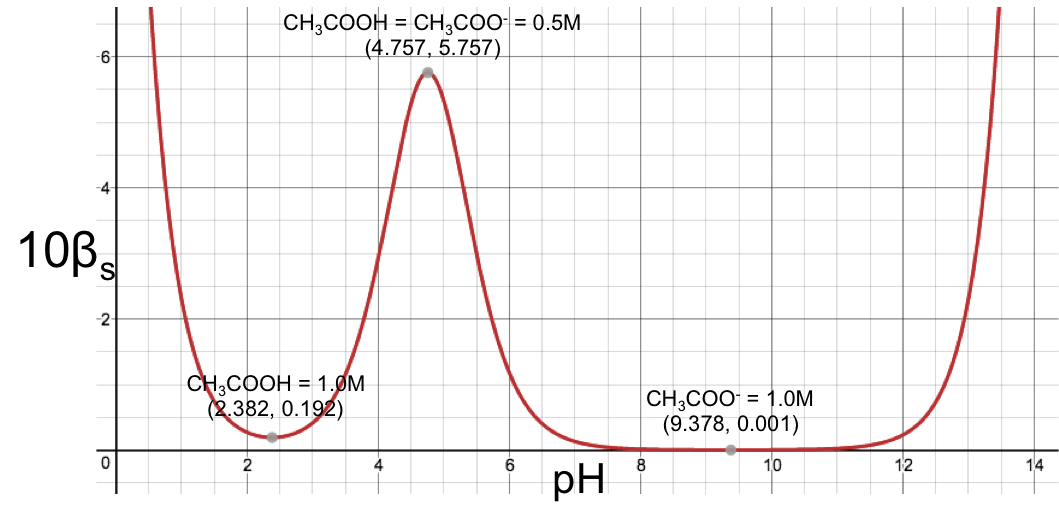
and using eq16 to plot a graph of βs versus pH for 1.0 M aqueous ethanoic acid (Ka = 1.75 x 10-5) :
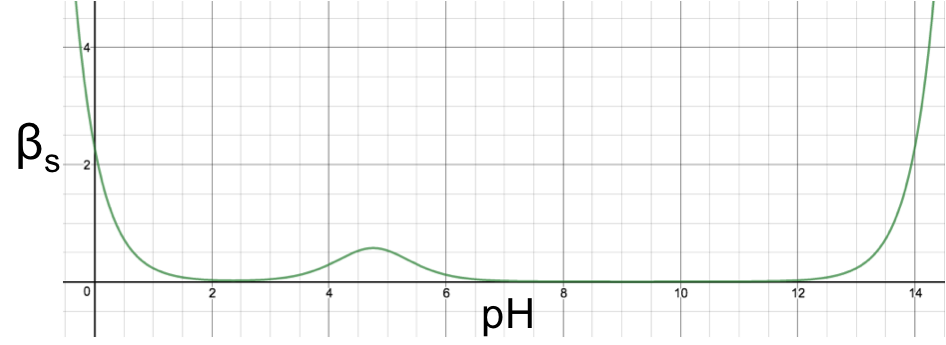
The graph shows a maximum point at (4.757,0.576) corresponding to the maximum buffer capacity at pH = 4.757, which is attributed to the ethanoic acid/ethanoate buffer pair; while the increased in buffer capacity below pH 2 and above pH 12 is attributed to water. If we scale the graph by multiplying eq16 throughout by a factor of 10 and plotting 10βs versus pH, we observe another two stationary points (minimum points), each corresponding to the sum of the minimum buffer capacity of the weak acid and the increased buffer capacity of water: