A complete vector space is one that has no “missing elements” (e.g. no missing coordinates).

In the previous article, we learned that the function defines the distance between two elements of the vector space. Such a function is called a metric and it measures the ‘closeness’ of elements (or points) in a vector space. Since a vector space is a collection of elements, we can use a sequence, e.g.
, to represent elements of a vector space
. If the distance between two members of the sequence gets closer as
gets larger (see diagram below), i.e.
we call the sequence a Cauchy sequence.
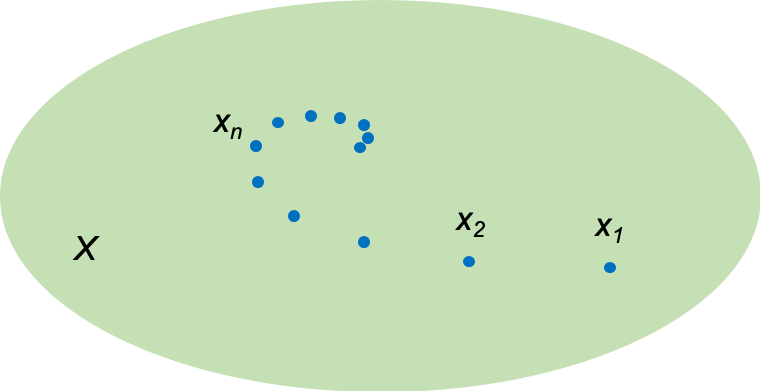
Cauchy sequences are useful in determining the completeness of a vector space. A vector space is complete if every Cauchy sequence in
converges to an element of
. For example, the sequence
, where
, is one of many Cauchy sequences of rational numbers in the rational number space
. However, the sequence converges to
, which is not an element of
. Therefore,
is not complete, and has “missing elements” or “gaps”, as compared to the real space number space
, which is complete.

Question
Show that .
Answer
If , then
. So,
or
Integrating the 2nd equality of the above equation on both sides, we have
Substituting in the above equation, we have
.
A vector space with no “missing elements” is essential for scientists to work with to formulate theories (e.g. kinematics) and solving problems associated with those theories. Furthermore, the ability to compute limits in a complete vector space implies that we can apply calculus to solve problems defined by the space. For example, a complete inner product space called a Hilbert space, which will be discussed in the next article, is used to formulate the theories of quantum mechanics.