Basis

A basis of a group is a set of objects that transforms according to representations of the group. The objects may be vectors, pseudovectors, functions, bond angles, etc. They are not necessarily orthogonal but are usually chosen to be orthogonal for certain applications.

To explain the definition of a basis, we consider the $C_{2v}$ point group with the following character table:

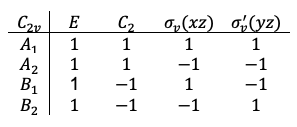
Let’s examine how symmetry operators of $C_{2v}$ transform $p$ -orbital wavefunctions.

$\psi_{p_z}$ , by inspection, is invariant when acted upon by each of the four symmetry operators of $C_{2v}$ (see diagram below). Mathematically, we obtain the same eigenvalue of +1 after each operation, e.g. $\hat{C}_{2}\psi_{p_z}=\psi_{p_z}$ . We say that $\psi_{p_z}$ transforms according to the totally symmetric representation $A_1$ . Repeating the logic, $\psi_{p_x}$ and $\psi_{p_y}$ transform according to $B_1$ and $B_2$ respectively.

As we know,

$\psi_{p_z}=zf(r)\;\;\;\psi_{p_x}=xf(r)\;\;\;\psi_{p_y}=yf(r)$

where $f(r)=\frac{1}{4\sqrt{2\pi}}\sqrt{\biggr$\frac{1}{a}\biggr$^5}e^{-\frac{r}{2a}}$ and $r$ is the distance from the origin. Hence, the function $f(r)$ is invariant to all symmetry operations of a point group. This implies that the $p$ -orbital wavefunctions transform in the same way as the linear functions $\psi_{p_z}=z$ , $\psi_{p_x}=x$ and $\psi_{p_y}=yf(r)$ . We call these functions basis functions and include them in the character table as follows:

The basis functions $x$ , $y$ and $z$ in the character table of a point group also represent the independent translational motions of a molecule of that point group. To elaborate further, let’s define the independent translational motions of a molecule as the displacement of the molecule in the $x$ , $y$ and $z$ directions. For example, the diagram below describes the displacement of $H_2O$ in the $z$ -direction in terms of unit instantaneous displacements vectors that are centred on the atoms, or equivalently, a single instantaneous displacement vector on the centre of mass.

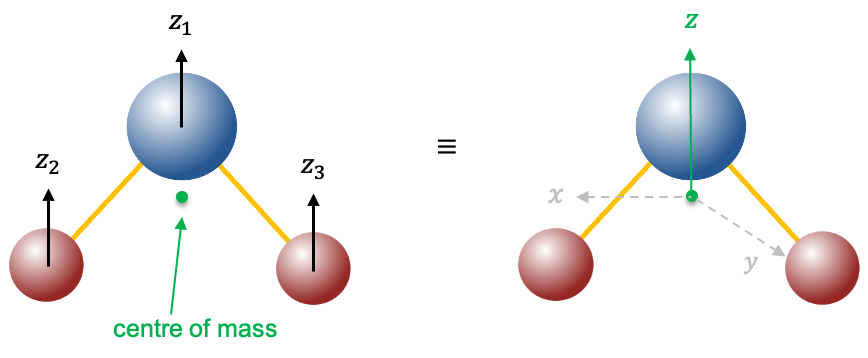
Similarly, the translational motions of $H_2O$ in the $x$ -direction and $y$ -direction are described by corresponding displacement vectors on the centre of mass. These three linearly independent displacement vectors form a basis set of a representation $\Gamma_R$ of $C_{2v}$ because any one of the vectors is transformed by the symmetry operations of $C_{2v}$ into a linear combination of the vectors in the set. Symmetry operations acting on the basis set produce the following results:

$\{x,y,z\}\xrightarrow{E}\{x,y,z\}$	$\{x,y,z\}\xrightarrow{\sigma_v}\{x,-y,z\}$
$\{x,y,z\}\xrightarrow{C_2}\{-x,-y,z\}$	$\{x,y,z\}\xrightarrow{\sigma_v^{'}}\{-x,y,z\}$

The corresponding matrix transformation equations are:

$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}$	$\begin{pmatrix}x\\-y\\z\end{pmatrix}=\begin{pmatrix}1&0&0\\0&-1&0\\0&0&1\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}$
$\begin{pmatrix}-x\\-y\\z\end{pmatrix}=\begin{pmatrix}-1&0&0\\0&-1&0\\0&0&1\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}$	$\begin{pmatrix}-x\\y\\z\end{pmatrix}=\begin{pmatrix}-1&0&0\\0&1&0\\0&0&1\end{pmatrix}\begin{pmatrix}x\\y\\z\end{pmatrix}$

The $3\times 3$ transformation matrices form $\Gamma_R$ , which is reducible and in block-diagonal form, with $x$ , $y$ and $z$ transforming according to $B_1$ , $B_2$ and $A_1$ respectively. Therefore, the bases $x$ , $y$ and $z$ in the $C_{2v}$ character table represent the independent translational motions of $H_2O$ .

We can also use instantaneous displacement vectors to describe rotational motions of a molecule. The rotation of $H_2O$ about the $y$ -axis is shown in the diagram below, with three instantaneous displacement vectors tangent to the two circular paths of motion.

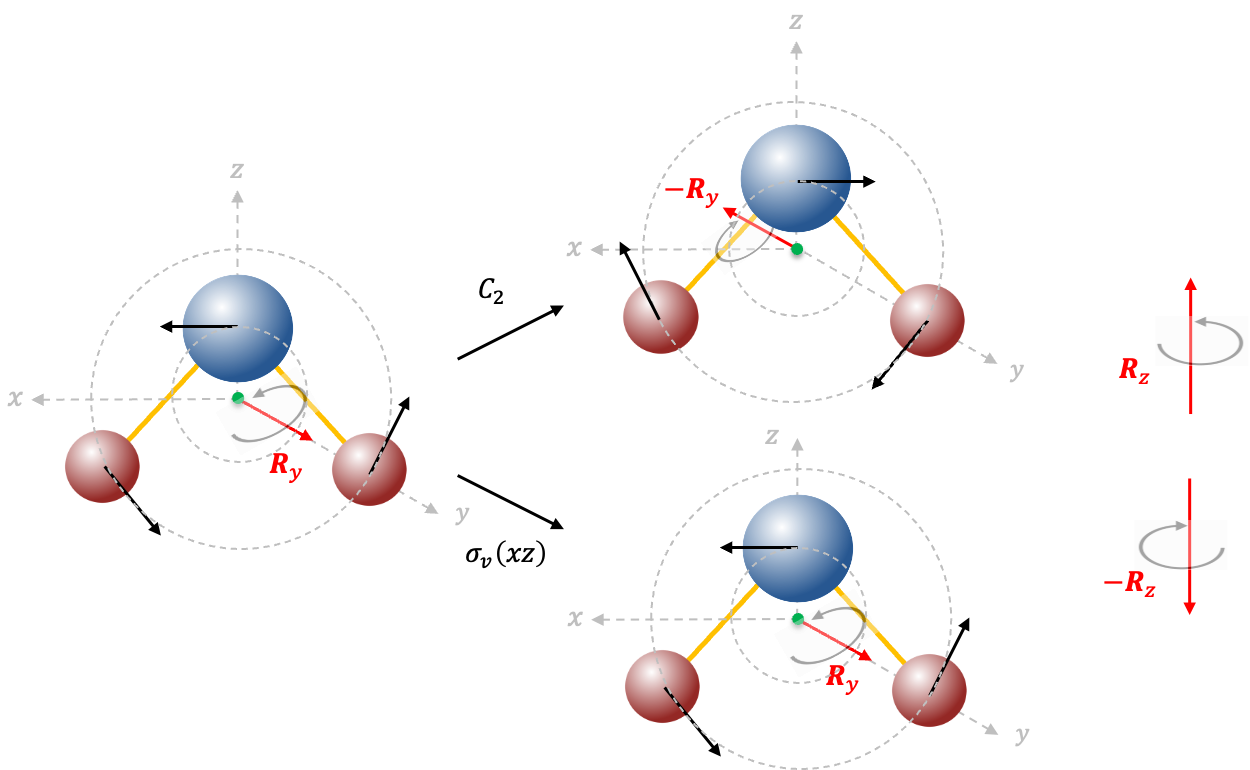
Just like the way we reduce the three translational displacement vectors to a single vector centred on the centre of mass of $H_2O$ , we represent the three rotational vectors with $\boldsymbol{\mathit{R}}_y$ , which is a pseudovector characterised by two quantities: a rotation direction that is defined by the right-hand rule and a magnitude that represents the rotation angle $\theta$ . Therefore, the transformation of the three instantaneous vectors by the $C_2$ symmetry operation is equivalent to the reflection of the rotation direction of $\boldsymbol{\mathit{R}}_y$ (curved grey arrow) about the $xz$ plane. The $\sigma_v$ symmetry operation leaves the instantaneous vectors, and hence the rotation direction of $\boldsymbol{\mathit{R}}_y$ , unchanged.

Symmetry operations acting on the basis set $\{\boldsymbol{\mathit{R}}_x,\boldsymbol{\mathit{R}}_y,\boldsymbol{\mathit{R}}_z\}$ produce the following results:

$\{\boldsymbol{\mathit{R}}_x,\boldsymbol{\mathit{R}}_y,\boldsymbol{\mathit{R}}_z\}\xrightarrow{E}\{\boldsymbol{\mathit{R}}_x,\boldsymbol{\mathit{R}}_y,\boldsymbol{\mathit{R}}_z\}$	$\{\boldsymbol{\mathit{R}}_x,\boldsymbol{\mathit{R}}_y,\boldsymbol{\mathit{R}}_z\}\xrightarrow{\sigma_v}\{-\boldsymbol{\mathit{R}}_x,\boldsymbol{\mathit{R}}_y,-\boldsymbol{\mathit{R}}_z\}$
$\{\boldsymbol{\mathit{R}}_x,\boldsymbol{\mathit{R}}_y,\boldsymbol{\mathit{R}}_z\}\xrightarrow{C_2}\{-\boldsymbol{\mathit{R}}_x,-\boldsymbol{\mathit{R}}_y,\boldsymbol{\mathit{R}}_z\}$	$\{\boldsymbol{\mathit{R}}_x,\boldsymbol{\mathit{R}}_y,\boldsymbol{\mathit{R}}_z\}\xrightarrow{\sigma_v^{'}}\{\boldsymbol{\mathit{R}}_x,-\boldsymbol{\mathit{R}}_y,-\boldsymbol{\mathit{R}}_z\}$

The corresponding matrix transformation equations are:

$\begin{pmatrix}\boldsymbol{\mathit{R}}_x\\\boldsymbol{\mathit{R}}_y\\\boldsymbol{\mathit{R}}_z\end{pmatrix}=\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}\begin{pmatrix}\boldsymbol{\mathit{R}}_x\\\boldsymbol{\mathit{R}}_y\\\boldsymbol{\mathit{R}}_z\end{pmatrix}$	$\begin{pmatrix}-\boldsymbol{\mathit{R}}_x\\\boldsymbol{\mathit{R}}_y\\-\boldsymbol{\mathit{R}}_z\end{pmatrix}=\begin{pmatrix}-1&0&0\\0&1&0\\0&0&-1\end{pmatrix}\begin{pmatrix}\boldsymbol{\mathit{R}}_x\\\boldsymbol{\mathit{R}}_y\\\boldsymbol{\mathit{R}}_z\end{pmatrix}$
$\begin{pmatrix}-\boldsymbol{\mathit{R}}_x\\-\boldsymbol{\mathit{R}}_y\\\boldsymbol{\mathit{R}}_z\end{pmatrix}=\begin{pmatrix}-1&0&0\\0&-1&0\\0&0&1\end{pmatrix}\begin{pmatrix}\boldsymbol{\mathit{R}}_x\\\boldsymbol{\mathit{R}}_y\\\boldsymbol{\mathit{R}}_z\end{pmatrix}$	$\begin{pmatrix}\boldsymbol{\mathit{R}}_x\\-\boldsymbol{\mathit{R}}_y\\-\boldsymbol{\mathit{R}}_z\end{pmatrix}=\begin{pmatrix}1&0&0\\0&-1&0\\0&0&-1\end{pmatrix}\begin{pmatrix}\boldsymbol{\mathit{R}}_x\\\boldsymbol{\mathit{R}}_y\\\boldsymbol{\mathit{R}}_z\end{pmatrix}$

The $3\times 3$ transformation matrices form $\Gamma_R$ , which is again reducible and in block-diagonal form, with $\boldsymbol{\mathit{R}}_x$ , $\boldsymbol{\mathit{R}}_y$ and $\boldsymbol{\mathit{R}}_z$ transforming according to $B_2$ , $B_1$ and $A_2$ respectively. Therefore, the bases $\boldsymbol{\mathit{R}}_x$ , $\boldsymbol{\mathit{R}}_y$ and $\boldsymbol{\mathit{R}}_z$ in the $C_{2v}$ character table represent the independent rotational motions of $H_2O$ .

As such, we can revise the character table:

$d$ -orbitals wavefunctions, which are quadratic polynomials, also form a basis. For example, the $d_{xy}$ orbital wavefunction transforms according to $A_2$ (see diagram below).

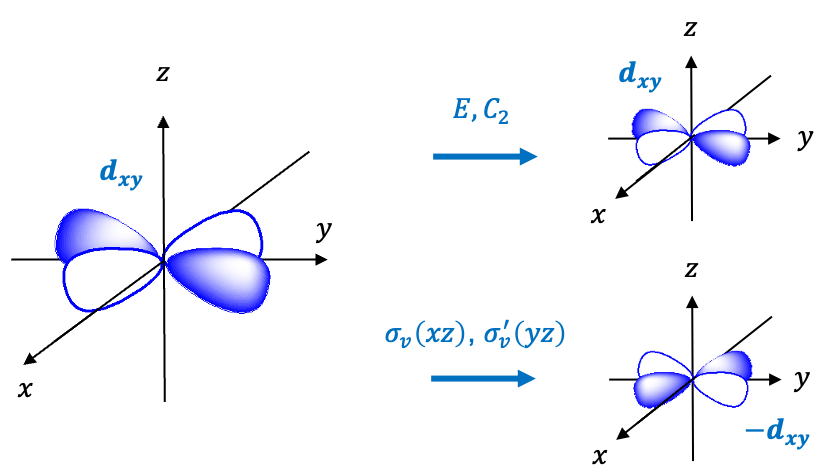
Consequently, we have

Question

Can $f$ -orbital wavefunctions form a basis for a group?

Answer

Yes, they are classified as a basis of cubic functions.

Lastly, character tables for some point groups have certain elements of a basis in parentheses. An example is the $C_{3v}$ point group:

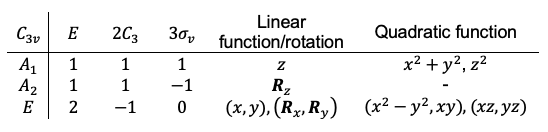
which in the matrix representation form is

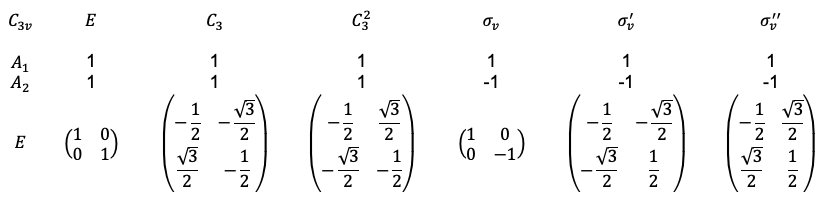
The notation of $(i,j)$ means that $i$ and $j$ transform together but not independently under a symmetry operation. To elaborate on this, let’s consider the wavefunctions $\psi_{p_x}$ and $\psi_{p_y}$ . Separately, each wavefunction does not transform according to any of the three irreducible representations of $C_{3v}$ . This can be verified by letting any point on any of the wavefunctions undergo the $C_{3}$ symmetry operation. The eigenvalue obtained does not match any element of any irreducible representation of $C_{3v}$ .

However, if we subject both wavefunctions together to the symmetry operation $C_{3}$ , e.g. by choosing the points $x_1=\begin{pmatrix}1\\0\end{pmatrix}$ and $y_1=\begin{pmatrix}0\\1\end{pmatrix}$ on $\psi_{p_x}$ and $\psi_{p_y}$ respectively (see diagram below), we obtain, after some simple geometry, the transformed points $x_2=\begin{pmatrix}-\frac{1}{2}\\\frac{\sqrt{3}}{2}\end{pmatrix}$ and $y_2=\begin{pmatrix}-\frac{\sqrt{3}}{2}\\-\frac{1}{2}\end{pmatrix}$ .

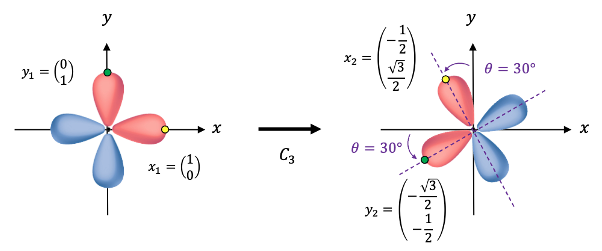
In matrix form, we have

$\hat{C}_3\begin{pmatrix}1&0\\0&1\end{pmatrix}=\begin{pmatrix}-\frac{1}{2}&-\frac{\sqrt{3}}{2}\\\frac{\sqrt{3}}{2}&-\frac{1}{2}\end{pmatrix}\begin{pmatrix}1&0\\0&1\end{pmatrix}$

or, in a new notation,

$\hat{C}_3(x,y)=\begin{pmatrix}-\frac{1}{2}&-\frac{\sqrt{3}}{2}\\\frac{\sqrt{3}}{2}&-\frac{1}{2}\end{pmatrix}(x,y)$

Repeating the same logic for the rest of the symmetry operators and comparing the results with the table depicting the matrix representation of $C_{3v}$ , we find that the wavefunctions $\psi_{p_x}$ and $\psi_{p_y}$ , which are equivalent to the basis functions $x$ and $y$ , transform together according to the irreducible representation $E$ . We also find that a basis can be used to give rise to matrix representations of a group, since the matrix form of $C_{3}$ is generated in the process.

Using the same logic for the rotation vectors and the $d$ -orbitals, we find that the pairs $(\boldsymbol{\mathit{R}}_x,\boldsymbol{\mathit{R}}_y)$ , $(x^2-y^2,xy)$ and $(xz,yz)$ transform according to the irreducible representation $E$ .

An important implication of the basis functions $x$ and $y$ transforming together under the symmetry operations of a particular point group is that there is no difference in symmetry between them with respect to that point group. In other words, the two basis functions and certain properties they possess may be treated as equivalent and indistinguishable. An example is the common energy state that corresponds to $\psi_{p_x}$ and $\psi_{p_y}$ , i.e. a degenerate energy state. Therefore, group theory plays a useful role in spectroscopic analysis.

Question

Answer

Next article: Symmetry of the Hamiltonian

Previous article: Character table

Content page of group theory

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply