Character table - Mono Mole

A character table is a square matrix whose rows and columns are irreducible representations $\Gamma_j$ of a point group $G$ and classes $C_{i}$ of $G$ , respectively, with the entries being the characters $\chi_j(C_i)$ of elements of the corresponding irreducible representation. It has the general form:

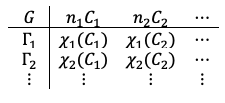
where $n_i$ is the number of elements in the $i$ -th class.

The construction of a character table is based on the following properties, some of which are related to the little orthogonality theorem:

1. There is always a one-dimensional irreducible representation, called a totally symmetric representation, in which all the characters are 1. It is conventionally denoted by $\Gamma_1$ . This is because a representation of a group is a collection of matrices that multiply according to the multiplication table of the group and the collection of $1\times 1$ matrices, each with entry 1, always multiply according to the multiplication table of that group.
2. The number of irreducible representations is equal to the number of classes of the group. This is a consequence of the 1^stlittle orthogonality relation.
3. The sum of the squares of the dimensions of all the irreducible representations of a group is equal to the order of the group, i.e. $\vert G\vert=\sum_kd_k^2$ , which is eq40.
4. Each irreducible representation is regarded as a basis vector in a $\vert G\vert$ -dimensional vector space, with the weighted characters of an irreducible representation being the components of the corresponding basis vector. Therefore, irreducible representations have orthonormal relations with one another. These relations are characterised by either
  a) $\sum_{\alpha=1}^C\sqrt{\frac{n_{\alpha}}{\vert G\vert}}\chi_k^*(\alpha)\sqrt{\frac{n_{\alpha}}{\vert G\vert}}\chi_{k'}(\alpha)=\delta_{kk'}$ (see eq24); or
  b) $\sum_{\alpha}\chi_k^*(\alpha)\chi_{k'}(\alpha)=\frac{\vert G\vert}{n_k}\delta_{kk'}$ (see eq24b)
5. The weighted sum of the squares of the characters of an irreducible representation is equal to the order of the group, i.e. $\sum_{\alpha}n_{\alpha}\vert \chi_k(\alpha)\vert^2=\vert G\vert$ , which is eq29.

For example, the character table for the $C_{3v}$ point group is constructed by first noting that there are six symmetry operations ( $\vert G\vert=6$ ) that belong to three classes. Using properties 1 and 2 mentioned above, there are three irreducible representations, with the first being the totally symmetric representation:

Using the 3^rd property, $6=1^2+d_2^2+d_3^2$ . Since $d_k\in\mathbb{N}$ , let $d_2=1$ and $d_3=2$ . Furthermore, the characters of a $1\times 1$ identity matrix and a $2\times 2$ identity matrix are 1 and 2 respectively. Therefore, we have

For orthogonal vectors $\Gamma_1$ and $\Gamma_2$ , property 4a states that

$\sqrt{\frac{1}{6}}(1)\sqrt{\frac{1}{6}}(1)+\sqrt{\frac{2}{6}}(1)\sqrt{\frac{2}{6}}\chi_{22}+\sqrt{\frac{3}{6}}(1)\sqrt{\frac{3}{6}}\chi_{23}=0$

$1+2\chi_{22}+3\chi_{23}=0\;\;\;\;\;\;\;\;41$

with the 5^th property requiring

$1+2\chi_{22}^2+3\chi_{23}^2=6\;\;\;\;\;\;\;\;42$

Since a representation of a group is a collection of matrices that multiply according to the multiplication table of the group, the $1\times 1$ matrices of $\Gamma_2$ (where the character itself is a matrix) must multiply according to the $C_{3v}$ multiplication table as follows:

In other words, $\chi_{23}^2=1$ and $\chi_{22}^2=\chi_{22}^2$ , where the elements (in matrix form) of the same class in a group have the same trace. Substituting $\chi_{23}^2=1$ and $\chi_{22}^2=\chi_{22}$ in eq42 gives $\chi_{22}=1$ ( $\chi_{22}=-1$ is rejected, see Q&A below for explanation), which substituted in eq41 gives $\chi_{23}=-1$ . We now have:

Question

1. How about the solution set of $\chi_{22}=-1$ and $\chi_{23}=\frac{1}{3}$ ?
2. Can we use the same logic in determining the characters of $\Gamma_2$ to derive the characters of $\Gamma_3$ ?

Answer

1. This solution set is rejected, as it is not consistent with property 5.
2. No, because we will end up with more variables than we can solve, e.g. for $C_3C_3=C_3^2$ , we have $\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}=\begin{pmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{pmatrix}$ , where $a_{11}+a_{22}=\chi_{32}$ and $b_{11}+b_{22}=\chi_{32}$ . Therefore, the method used to determine the characters of $\Gamma_2$ only works if $\Gamma_2$ is one-dimensional.

The remaining characters are obtained using property 4b, where $1\cdot 1+1\cdot 1+2\cdot\chi_{32}=0$ and $1\cdot 1+1\cdot (-1)+2\cdot\chi_{33}=0$ . Therefore, $\chi_{32}=-1$ and $\chi_{33}=0$ , with

The character table of a point group can also be generated using basis functions, which are defined in the next article. Some point groups, e.g. $C_3$ and $C_{3h}$ , have a two-dimensional irreducible representation that contains two rows of characters that are complex conjugates of each other ( $\epsilon=e^{i2\pi/n}$ ). Each of these rows of character is an irreducible representation in its own right, with the total number of irreducible representations equal to the number of classes of the group (property 2).

Finally, the generic irreducible representation symbols of $\Gamma_i$ are replaced by Mulliken symbols in character tables for clarity, where

1. $A$ : one-dimensional representation that is symmetric with respect to rotation about the principal axis, i.e. $\chi(C_n)=1$ .
2. $B$ : one-dimensional representation that is antisymmetric with respect to rotation about the principal axis, i.e. $\chi(C_n)=-1$ .
3. $E$ : two-dimensional representation (not to be confused with the identity element $E$ of the group)
4. $T$ : three-dimensional representation
5. If there are more than one $n$ -dimensional representation, subscripts $i=1,2,\cdots$ are used to differentiate them, e.g. $A_1$ and $A_2$ .
6. Molecular term symbols ( ${\sum}$ , $\Pi$ , $\Delta$ and $\Phi$ ), in addition to the Mulliken $A,B,E$ and $T$ , are used to label the irreducible representations of the axial point groups $C_{\infty v}$ and $D_{\infty h}$ . The molecular term symbol for an irreducible representation corresponds to the magnitude of the quantum number $m_l$ of a hydrogenic basis wavefunction that is used to generate the representation, e.g. $\Pi\leftrightarrow\psi_{p_x}=xf(r)$ , where $\vert m_l\vert=1$ . We have,
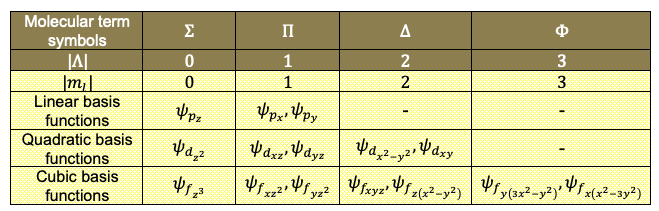  The use of molecular term symbols in character tables have useful applications in spectroscopy.
7. The subscript $g$ (from the German gerade, meaning even) refers to representations that are symmetric with respect to inversion, while the subscript $u$ (from the German ungerade, meaning uneven) refers to representations that are antisymmetric with respect to inversion.
8. The superscript ‘ refers to representations that are symmetric with respect to $\sigma_h$ , while the superscript ” refers to representations that are antisymmetric with respect to $\sigma_h$ .
9. The superscript + refers to representations that are symmetric with respect to $\sigma_v$ , while the superscript – refers to representations that are antisymmetric with respect to $\sigma_v$ .

So, we have

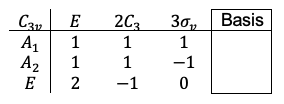
The last part of a character table lists basis functions that transform according to the irreducible representations of the group. We shall elaborate on this in the next article.

Next article: Basis

Previous article: Regular representation

Content page of group theory

Content page of advanced chemistry

Main content page

Question

Answer

Next article: Basis

Previous article: Regular representation

Content page of group theory

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply