The regular representation of a group is a reducible representation that is generated from a rearranged multiplication table of the group. It is used to derive an important property (see eq40 below) for constructing character tables.
Consider the re-arranged multiplication table for the point group such that all the identity elements are along the diagonal:
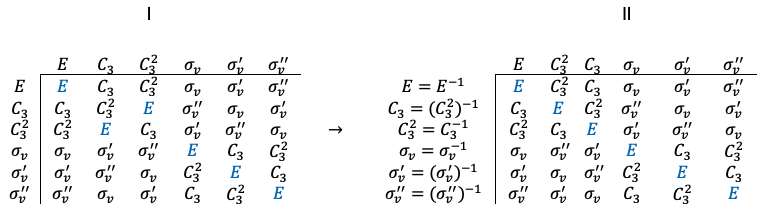
An element of the regular representation of the group is derived from table II in the form of a
matrix, whose entries are 1 when the element of
occurs in table II and zero otherwise. For example,
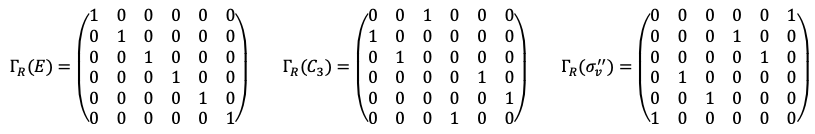
In other words, we have
where is the
-th row and
-th column matrix entry of the
-th element of the
representation of
.

Question
Show that each matrix of the regular representation of the point group has an inverse.
Answer
The entry 1 appears only once in every row (or column) of a matrix, e.g. , of the regular representation. We can therefore swap the rows (or columns) of
to form
. According to determinant property 1,
and consequently, according to determinant property 8,
. Therefore,
is non-singular, according to determinant property 11. The same logic applies to the rest of the matrices.
If these derived matrices are truly elements of a representation of , then they must satisfy the closure property of
, i.e.
where
Therefore, in eq35 needs to be equal to
to satisfy eq32. To prove this, we multiply the condition
in eq31 on the left by
to give
. Similarly, we multiply the condition
in eq34 on the left by
and then on the right by
to give
. Combining the two results, we have
, which when multiplied on the right by
and then on the left by
, gives
, which completes the proof.
By inspecting table II, the character of the regular representation is

Question
Show that the regular representation is reducible.
Answer
If the regular representation is reducible, the LHS of eq28 must be greater than . Applying the LHS of eq28 to the regular representation and using eq36,
For non-single element groups, and hence
.
Finally, we shall prove that . From eq25 and eq27, we have
where and
are the characters for the
-th class of the regular representation and irreducible representation respectively.
Expanding eq38 and using eq36,

Question
Why is ?
Answer
The regular representation for is a reducible representation that is the direct sum of irreducible representations under the class
. Each of these constituent irreducible representations is in general a
matrix with trace of
.
Eq39 therefore states that each constituent irreducible representation occurs in the regular representation a number of times that is equal to the dimension of the corresponding irreducible representation. For example, with reference to the table below,
, where
,
and
. In other words, each of the irreducible representations
and
appears once in the
regular representation matrix element
, while the irreducible representation
appears twice.
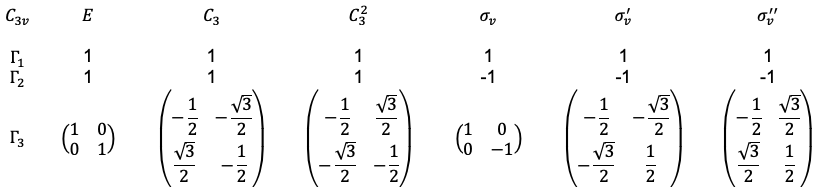
Since the matrix dimension for each element of the regular representation is ,
where we have used eq39 and where refers to the dimension of the
-th irreducible representation of a group.