The Rayleigh-Jeans law is a flawed attempt in physics to describe the spectral radiance of electromagnetic radiation as a function of wavelength from a blackbody at a given temperature.
Consider a cube of side , filled with electromagnetic radiation in thermal equilibrium at temperature
. If a tiny aperture exists in one of the walls, the radiation that it emits would exhibit the properties of an ideal blackbody. The walls, regarded as perfect conductors, provide boundary conditions for the electromagnetic waves inside the cube.
In a perfect conductor, an idealised model for real metals, electric charges can move without any resistance. An electromagnetic wave propagating in the -direction, with its electric field vector parallel to the wall, causes electrons in the conductor to move in response to the field. The movement of these electrons creates an opposing electric field that cancels out the external electric field. Given that the electric field is zero at the walls, the boundary conditions can only be satisfied by standing waves. These are waves that oscillate in place and have nodes at the cube’s walls. For example, standing waves oscillating in the
-direction have wavelengths of
, where
is an integer (see below diagram).
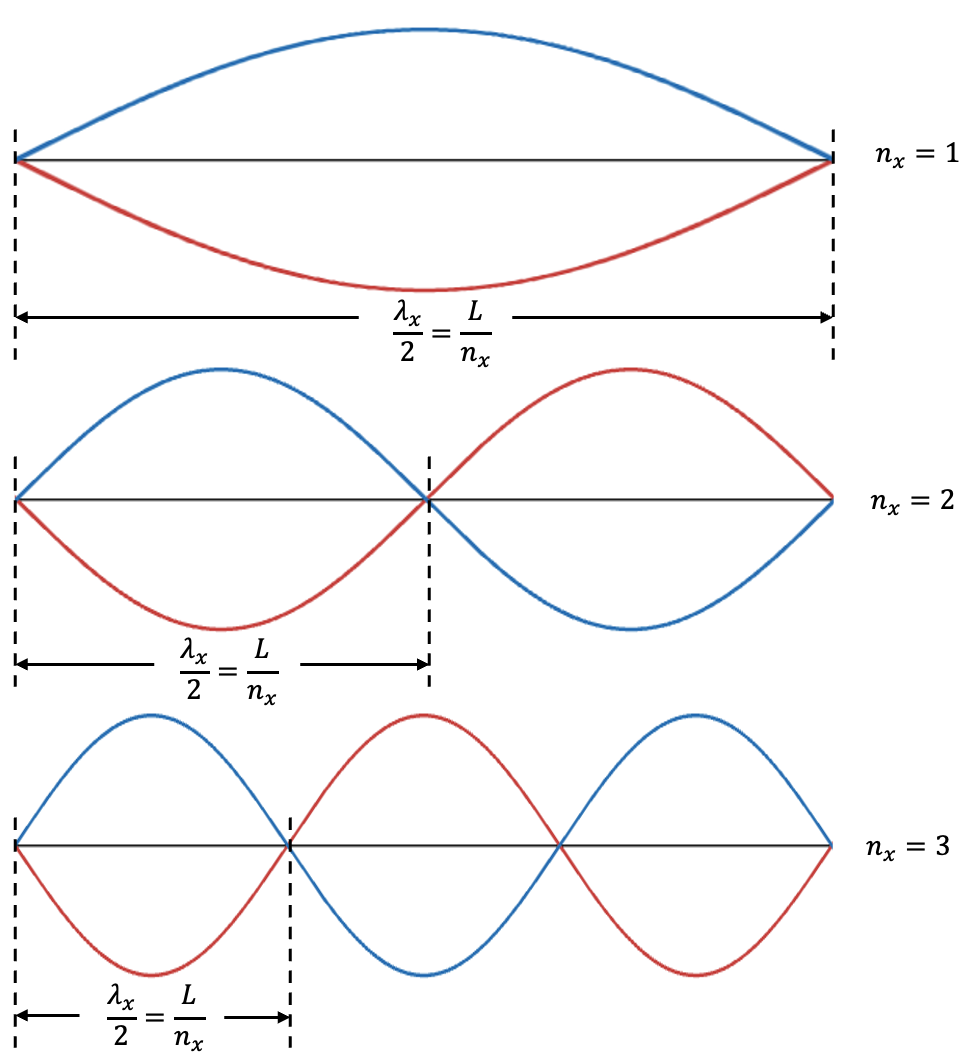
The amplitude of each of the above standing waves can be expressed as
, or in terms of the wave vector
pointing in the
-direction:
where .
Similarly, the wavelengths of the oscillation modes of the electromagnetic field in the -direction and
-direction are
and
respectively. Correspondingly, the magnitudes of the wave vectors are given by
and
respectively. It follows that the wave vector
of the oscillation modes of the electromagnetic field in an arbitrary direction in the cube lies in a
-space, which contain a cubical array of points that are
apart (see Figure I below).
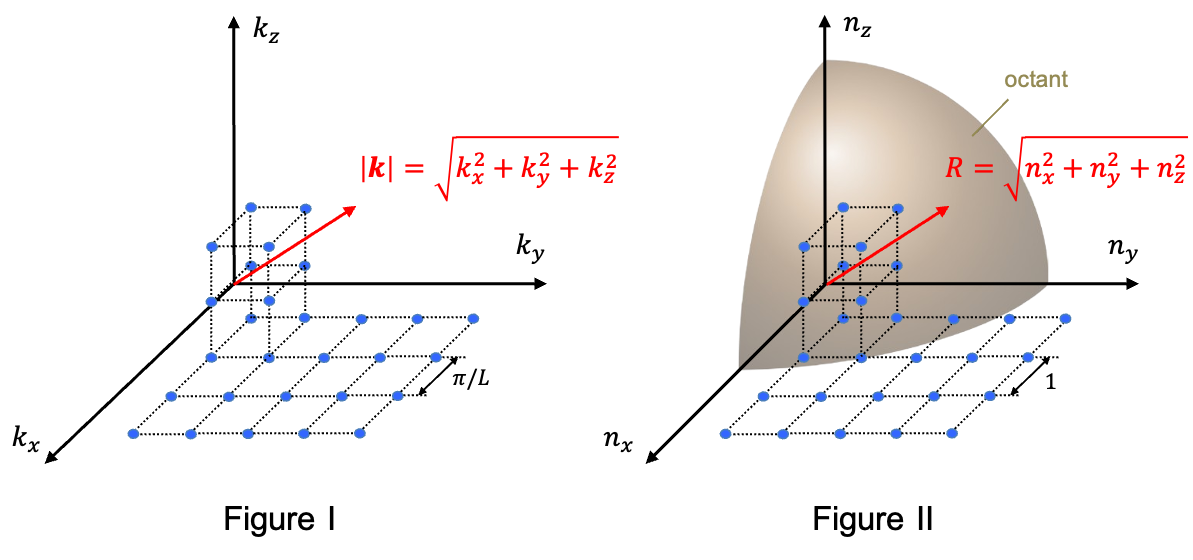
Since the magnitude of the wave vector is
, boundary conditions are satisfied by each ordered triple
. In other words, every mode of oscillation of an arbitrary wave oscillating in the cube is defined by a point in the
-space. We can also plot the array of modes in an
-space, where the points are now unit length apart from one another (see Figure II above). Substituting
in
, we have
where is the radius of an octant (one-eighth of the volume of a sphere) in the
-space.
For a certain value of , ordered triples of
that satisfy eq1 lie on the surface of the octant. Consider the volume of the shell of the octant
enclosed by the surfaces at
and
. Substituting eq1 and
in
, we have
Since the density of the number of modes in the
-space is one per unit volume, the number of modes
within the shell is the product of
and
:

As there are two independent polarisations for each mode of an electromagnetic wave (see above diagram),
Lord Rayleigh used the equipartition theorem to assume that each mode has an average energy of . Multiplying the above equation by the average energy
per mode, we have
where is the energy density (average energy per mode between
and
per unit volume of the cube).
Eq2 is known as the Rayleigh-Jeans law, which fails to describe the spectrum of blackbody radiation at high frequencies because it implies that radiated energy would increase without limit as increases, leading to what is called an ultraviolet catastrophe (see diagram below).
