Group theory plays a pivotal role in understanding molecular symmetry and electronic properties in organic chemistry, particularly when applied to the Hückel method.
Consider the benzene molecule. As the Hückel method is based on the -electron approximation, which treats
electrons separately from
electrons, the six
carbon orbitals of benzene are used as a basis to generate a representation of the
point group, which the molecule belongs to.

By selecting these six orbitals as a basis, their corresponding wavefunctions form a set of linearly independent wavefunctions that satisfy the effective Hamiltonian
of the
-electron approximation of benzene. This implies that any linear combination of these six wavefunctions is associated with an eigenvalue of
. Since molecular orbitals (MOs) are formed by the combination of atomic orbitals, these linear combinations represent MOs. To generate a set of orthogonal MOs of
, we let the
symmetry operations act on the basis set to produce the following results:
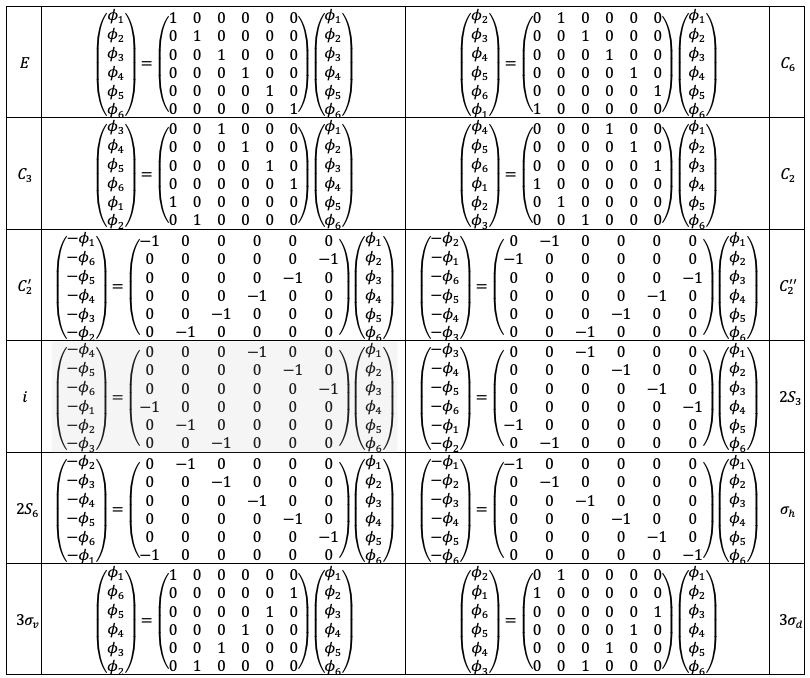
The transformation matrices form a reducible representation of the point group with the following traces:
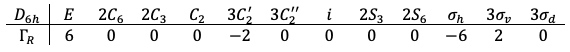
Using eq27a, is decomposed to
.
In other words, the matrices of can undergo a similarity transformation to yield block-diagonal matrices of the same form. Each block-diagonal matrix is composed of the direct sum of the four irreducible representations
,
,
and
. Since the number of orthogonal basis functions of an irreducible representation corresponds to the dimension of the representation, there are a total of six orthogonal basis functions for
(one each for
and
, and two each for
and
). These six basis functions can be generated using the projection operator.
Applying the projection operator on any -orbital wavefunction, for instance
, for the 1-dimensional irreducible representations of
and
, we have
As there are two basis functions each for the 2-dimensional irreducible representations and
, we apply the projection operator on two
-orbital wavefunctions, for instance
and
, to give
Some of these symmetry-adapted linear combinations (SALCs) are not orthogonal to one another. As linear combinations of basis functions that transform according to an irreducible representation of a point group also belong to the same irreducible representation, we can take linear combinations of and
(and
and
) to produce four SALCs that are orthogonal to
and
. The six orthogonal SALCs, after normalisation, are


Question
How do we normalise , where
is a constant?
Answer
Since , we have
.
The Hückel method assumes that
where
is known as the Coulomb integral if
.
is known as the resonance integral if
.
is the normalisation expression of
if
.
is known as the overlap integral if
.
To solve for the energies of
-electron MOs, we refer to eq157 of the Hartree-Fock-Roothaan method. The total wavefunction is
, where
is the antisymmetriser and
. Non-trivial solutions are given by the secular determinant:
is known as the Coulomb integral if
.
is known as the resonance integral if
.
is the normalisation expression of
if
.
is known as the overlap integral if
.
is the eigenvalue associated with
.

Question
Show that .
Answer
Expanding the integral and using the Hückel assumptions, we have . Similarly,
Eq109 becomes
Using the determinant identity , we multiply both sides of the above equation by
to give
where .
Using the determinant identity if
is diagonal, we have
. Therefore,
,
,
,
,
and
, giving the following MO diagram:
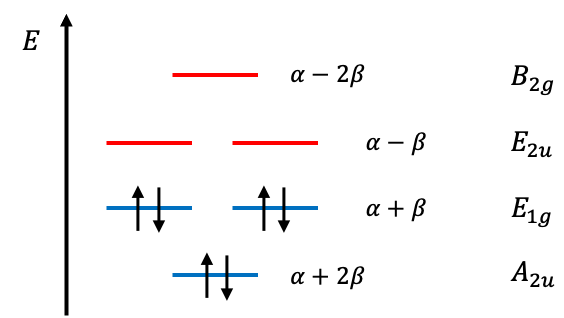
The total ground state electronic energy of benzene is
. If we regard two
electrons in benzene as localised between carbons atoms 1 and 2, another two between 3 and 4, and another two between 5 and 6, we can compare the total ground state
electronic energy of benzene with that of three molecules of ethene. The difference of
implies an energy stabilisation for benzene that is due to the delocalisation of electrons over the benzene ring, rather than being localised.