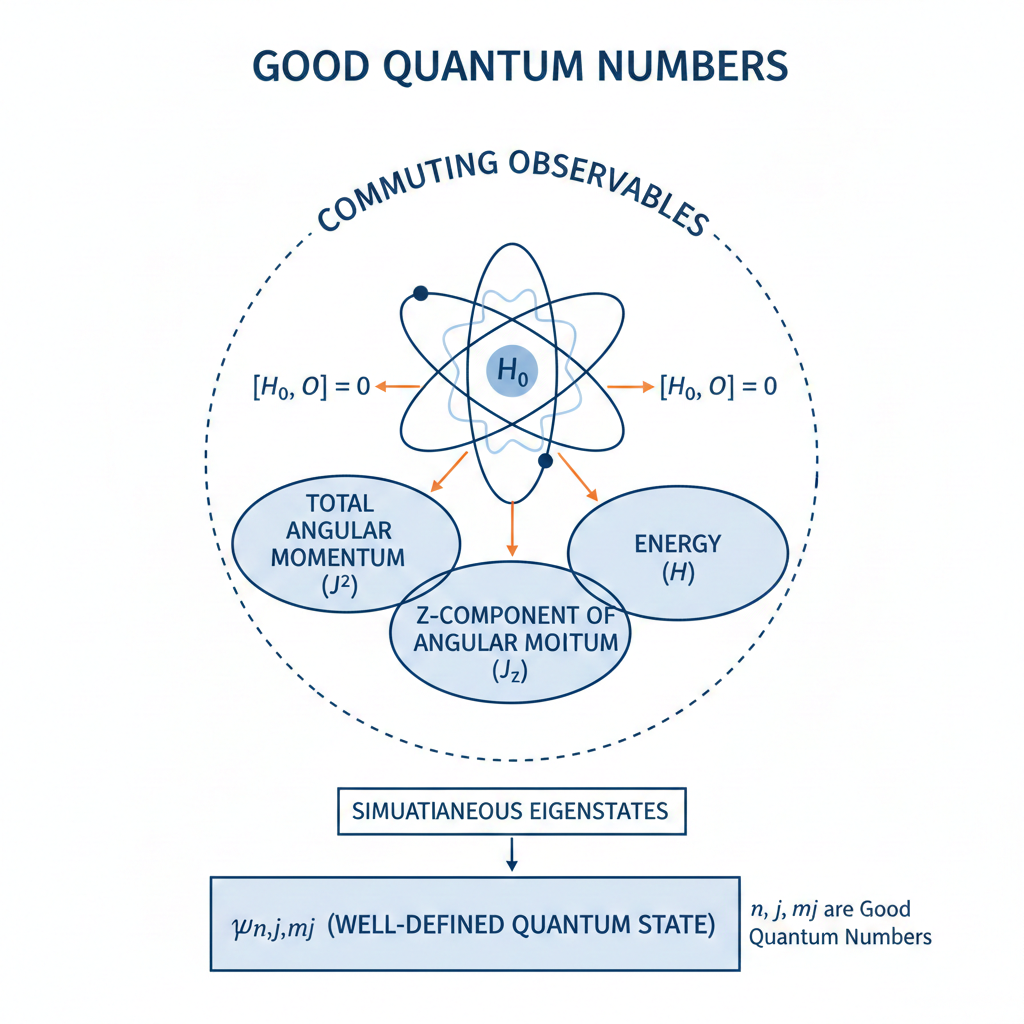
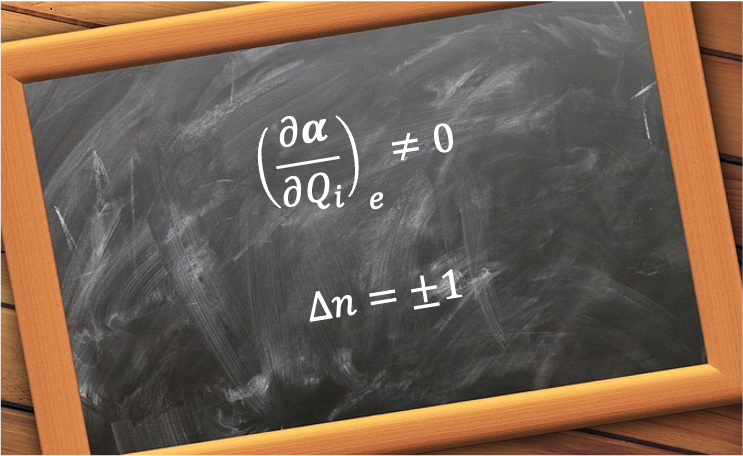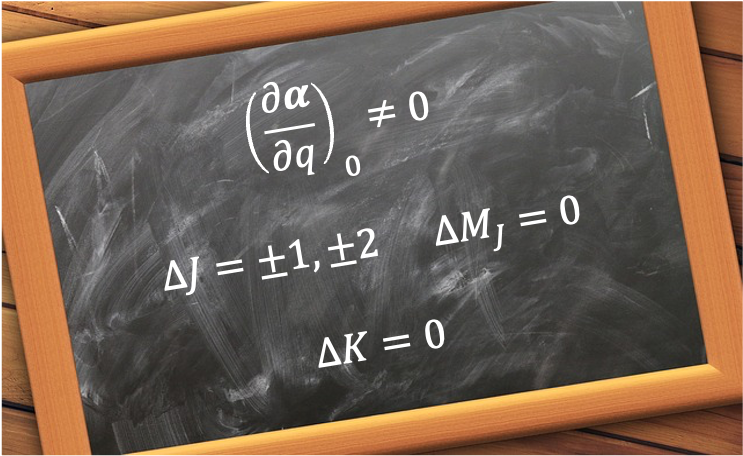A good quantum state is an eigenstate of the system Hamiltonian whose associated quantum numbers are conserved and uniquely label the state.

Such states arise from the symmetries of the Hamiltonian. As eigenstates of the Hamiltonian, they are unchanged under time evolution apart from an overall phase and provide a stable basis for describing physical observables and selection rules by enabling the diagonalisation of the Hamiltonian.
For example, a hydrogen atom is described by the good quantum state if spin-orbit coupling is ignored. The principal quantum number
counts the number of radial nodes in the electron wavefunction, which is fixed for a given energy level. Therefore,
remains conserved, and energy shells labeled by
are always well-defined, making it a good quantum number. The remaining quantum numbers are also good quantum numbers because their corresponding operators commute with the Hamiltonian
. We refer to
as an uncoupled basis state.

Question
Show that ,
and
commute with the Hamiltonian.
Answer
For and
, see the Q&A in this article by replacing
and
with
and
.
The non-relativistic Hamiltonian involves only spatial coordinates. Since
acts on a different Hilbert space (spin coordinate
), it always commutes with
:
However, when spin-orbit coupling is included, the Hamiltonian is given by , where
is the non-relativistic Hamiltonian and
is the perturbation due to spin-orbit coupling. In this case,
and
are no longer good quantum numbers, and the system is described by the good quantum state
, known as the coupled basis state.
and
remain good because
is a weak perturbation that does not significantly mix energy states labelled by these quantum numbers.

Question
What is a mixing of energy states?
Answer
“Mixing” means that energy states are perturbed. These new energy levels can no longer be described by a stationary-state like , but instead by a linear combination, e.g.:
This new state does not have a single value for or
, making them “bad” quantum numbers.
As mentioned eariler, commutes with
. It also commutes with
because
So, and
is proportional to

Question
Why is ?
Answer
Since any operator commutes with itself, . For the 2nd term,
and
commute because they act on different Hilbert spaces (space vs spin). Expanding
gives:
Using the identity , we find that
. Substituting
into the 3rd term and applying the same logic yields
.
Since commutes with both
and
, we have
, with
being a good quantum number. It follows that
is a good quantum number because
.
In the presence of an external magnetic field, the classification of a quantum number as “good” or “bad” depends on which interaction dominates the physical behaviour of the system. The Hamiltonian for the hydrogen atom becomes:
where is the pertubration due to the Zeeman effect.
In a weak magnetic field, where , the spin-orbit interaction is the dominant perturbation and
remains a good quantum state. The weak Zeeman field slightly shifts these states but is too weak to significantly mix states of different
. In this sense,
may be regarded as a “mostly good” quantum number, allowing the energies to be calculated accurately using perturbation theory.
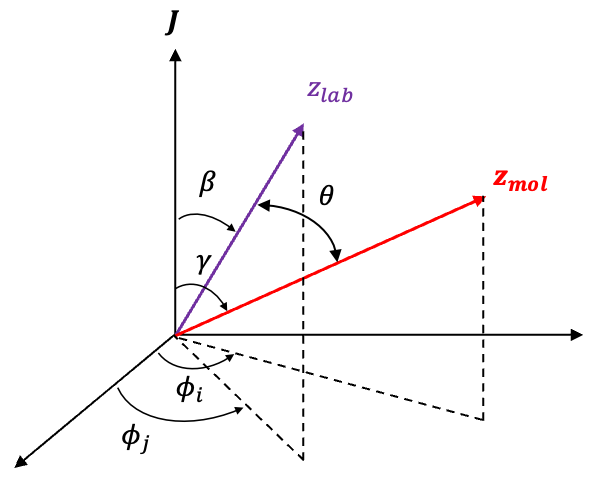
In a strong external magnetic field , torques are generated separately on the orbital and spin magnetic moments,
and
, with the vectors
and
antiparallel to
and
respectively. Each torque,
or
, is perpendicular to the external magnetic field direction (taken as the lab
-axis), so its component along the field axis is zero. Consequently, the projections
and
cannot change. The only way for
and
to evolve in time while maintaining constant projections onto the
-axis is for them to precess independently about the direction of the magnetic field. Hence,
and
become good quantum numbers again, and the state returns to the uncoupled form
.
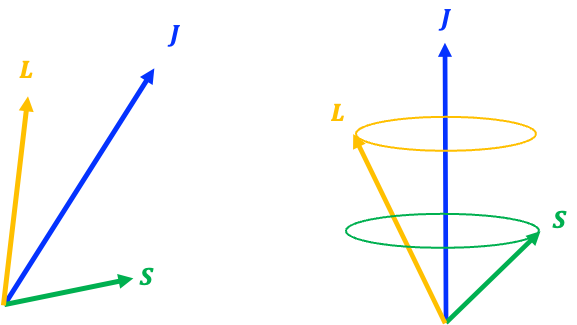

Question
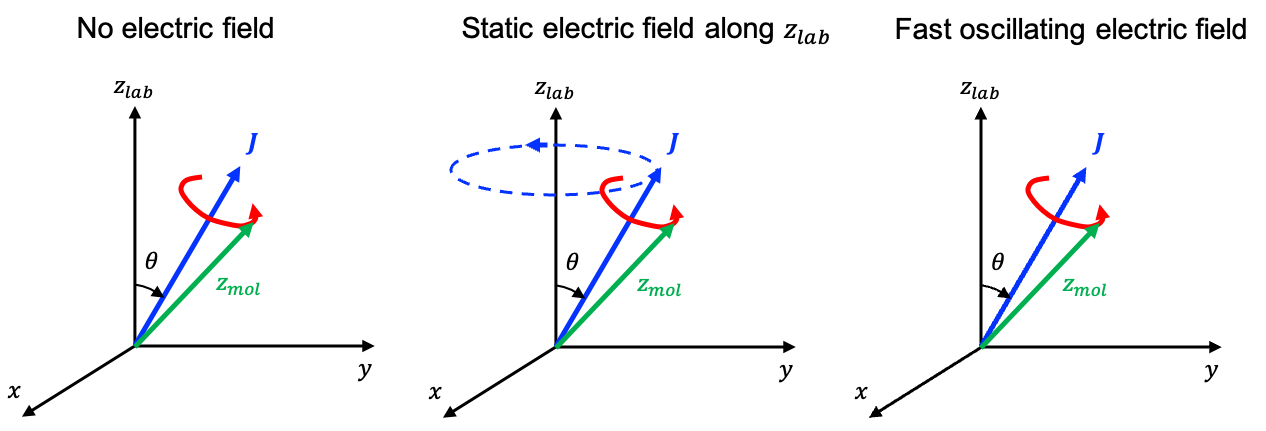
Does any precession occur in the hydrogen atom in the absence of an external magnetic field?
Answer
Yes, it does. In the rest frame of the electron, the positively charged nucleus orbits the electron. Since a moving charge creates a magnetic field, an internal magnetic field parallel to
is produced from the electron’s perspective by its own orbital motion.
interacts with the electron’s spin magnetic moment
, generating a torque:
Mathematically, this requires to precess about
. However, if
were constant while
precessed around it, the total angular momentum
would change. However, in an isolated atom,
must be conserved. To ensure this, an equal and opposite torque acts on
as the internal interaction pulls on
, causing both
and
to evolve in time. The only way for both
and
to change while keeping
constant is for them to precess about their vector sum
(see diagram above).
In the presence of a strong external magnetic field , the precessional motion due to the interaction of
with
becomes dominant, overwhelming the mutual precession of
and
around
. This leads to the decoupling of
and
.