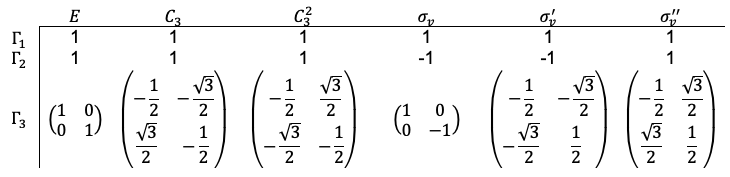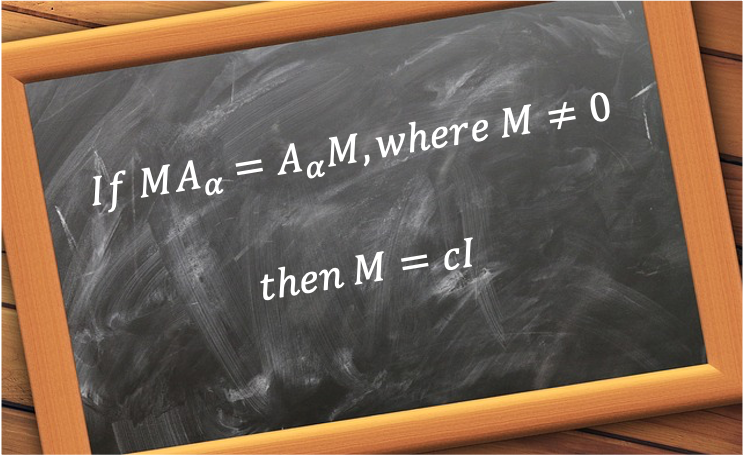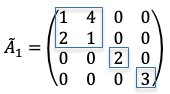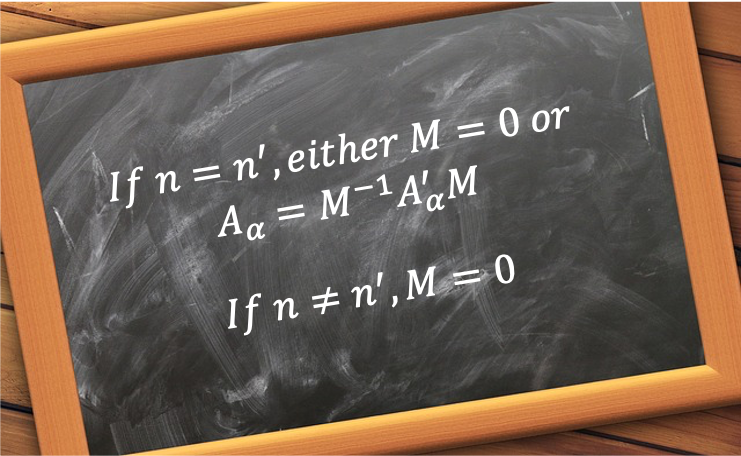The determinant is a number associated with an  matrix
matrix  . It is defined as
. It is defined as

where
-
 is an element of in the first row of
is an element of in the first row of  .
.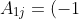^{1+j}M_{1j}^A) is the cofactor associated with
is the cofactor associated with  .
. , the minor of the element
, the minor of the element  , is the determinant of the
, is the determinant of the  matrix obtained by removing the
matrix obtained by removing the  row and
row and 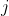 -th column of
-th column of  .
.
In the case of  , we say that the summation is a cofactor expansion along row 1. For example, the determinant of
, we say that the summation is a cofactor expansion along row 1. For example, the determinant of  is
is

For any square matrix, the cofactor expansion along any row and any column results in the same determinant, i.e.

To prove this, we begin with the proof that the cofactor expansion along any row results in the same determinant, i.e. 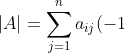^{i+j}M_{ij}^A) for
for  . Consider a matrix
. Consider a matrix 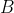 , which is obtained from
, which is obtained from  by swapping row
by swapping row 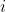 consecutively with rows above it
consecutively with rows above it 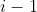 times until it resides in row 1. According to property 8 (see below), we have
times until it resides in row 1. According to property 8 (see below), we have
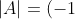^{i-1}\vert B\vert=(-1)^{i-1}\sum_{j=1}^nb_{1j}(-1)^{1+j}M_{1j}^B\\=(-1)^{i-1}\sum_{j=1}^na_{ij}(-1)^{1+j}M_{ij}^A=\sum_{j=1}^na_{ij}(-1)^{i+j}M_{ij}^A)
According to property 10,  and therefore, the cofactor expansion along any column also results in the same determinant. This concludes the proof.
and therefore, the cofactor expansion along any column also results in the same determinant. This concludes the proof.
In short, to calculate the determinant of an  matrix, we can carry out the cofactor expansion along any row or column. If we expand along a row, we have
matrix, we can carry out the cofactor expansion along any row or column. If we expand along a row, we have  . We then select any row
. We then select any row 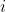 to execute the summation. Conversely, if we expand along a column, we get
to execute the summation. Conversely, if we expand along a column, we get  .
.
The following are some useful properties of determinants:
-
 , where is
, where is 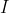 the identity matrix. If one of the diagonal elements of
the identity matrix. If one of the diagonal elements of 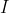 is
is 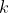 , then
, then  .
.
- If the elements of one of the columns of
 are all zero,
are all zero,  .
.
- If
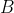 is obtained from
is obtained from  by multiplying the
by multiplying the 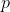 -th row of
-th row of  by
by 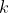 ,
,  .
.



- If
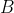 is obtained from
is obtained from  by swapping two rows or columns of
by swapping two rows or columns of  , then
, then 
- If two rows or two columns of
 are the same,
are the same,  .
.

- The inverse of a matrix exists only if
 .
.
- If
 , then
, then  .
.
- If
 , then
, then  . If
. If  , then
, then  .
.
- If
 is diagonal, then
is diagonal, then  .
.
Proof of property 1
We shall proof this property by induction.
For  ,
,

For 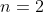 ,
,
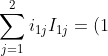(-1)^2M_{11}+(0)(-1)^3M_{12}=(1)(-1)^2(1)=1)
Let’s assume that for 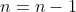 ,
,  . Then for
. Then for 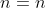 ,
,
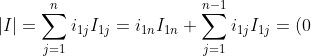I_{1n}+1=1)
We can repeat the above induction logic to prove that  if one of the diagonal elements of
if one of the diagonal elements of 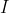 is
is 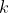 .
.
Proof of property 2
Again, we shall proof this property by induction.
For  ,
,

For 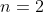 ,
,
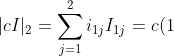(-1)^2M_{11}+c(0)(-1)^3M_{12}=c\vert ci_{22}\vert=c(c)=c^2)
Let’s assume that for 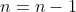 , we have
, we have  . Then for
. Then for 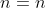 ,
,
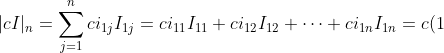I_{11}+c(0)I_{12}+\cdots+c(0)I_{1n}=cI_{11}=c\vert cI\vert_{n-1}=cc^{n-1}=c^n)
Proof of property 3
For 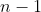 , where
, where  , we have
, we have  . For
. For 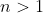 , the definition
, the definition  allows us to sum by row or by column. Suppose we sum by row, we have
allows us to sum by row or by column. Suppose we sum by row, we have  . Since we are allowed to choose any column
. Since we are allowed to choose any column 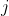 to execute the summation, we can always select the column
to execute the summation, we can always select the column 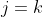 such that
such that  . Therefore,
. Therefore,  if the elements of one of the columns of are all zero.
if the elements of one of the columns of are all zero.
Proof of property 4
Let’s suppose 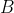 is obtained from
is obtained from  by multiplying the
by multiplying the 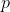 -th row of
-th row of  by
by 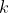 . If we expand
. If we expand  and
and  along row
along row 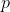 , cofactor
, cofactor  is equal to cofactor
is equal to cofactor  . Therefore,
. Therefore,

Proof of property 5
For a type I elementary matrix,  transforms
transforms  by swapping two rows of
by swapping two rows of  . So,
. So,  due to property 8. Since
due to property 8. Since  is obtained from
is obtained from 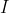 by swapping two rows of
by swapping two rows of 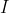 , we have
, we have  according to property 1 and property 8, which implies that
according to property 1 and property 8, which implies that  . Therefore,
. Therefore,  .
.
For a type II elementary matrix,  due to property 4 and
due to property 4 and  because of property 1. So,
because of property 1. So,  .
.
For a type III elementary matrix,
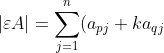A_{pj}=\sum_{j=1}^na_{pj}A_{pj}+k\sum_{j=1}^na_{qj}A_{pj}=\vert A\vert+k\vert B\vert)
 is computed by expanding along row
is computed by expanding along row 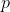 . The equation
. The equation  means that when
means that when  is computed by expanding along row
is computed by expanding along row 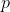 , it has the same cofactor as when
, it has the same cofactor as when  is computed by expanding along row
is computed by expanding along row 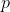 . This implies that
. This implies that  . Since the definition of the determinant of
. Since the definition of the determinant of 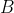 is
is  , which in our case is equivalent to
, which in our case is equivalent to  , we have
, we have  . Thus
. Thus  , which according to property 9, gives:
, which according to property 9, gives:

Since  ,
,

according to eq5 and property 1.
Comparing eq5 and eq6,  .
.
Proof of property 6
Case 1
If  is singular, where
is singular, where  , then
, then 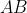 is also singular according to property 12. So,
is also singular according to property 12. So,  .
.
Case 2
If  is non-singular, it can always be expressed as a product of elementary matrices:
is non-singular, it can always be expressed as a product of elementary matrices:  . So,
. So,
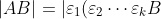\vert)
Since property 5 states that  ,
,

Similarly, 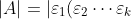\vert=\vert\varepsilon_1\vert\vert\varepsilon_2\vert\cdots\vert\varepsilon_k\vert) . Substitute this in the above equation,
. Substitute this in the above equation,  .
.
Proof of property 7
Using property 6 and then property 2,

Proof of property 8
We shall proof this property by induction. 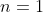 is the trivial case, where
is the trivial case, where  is the rank of a square matrix.
is the rank of a square matrix.
For 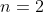 , let
, let  and
and  , which is obtained from
, which is obtained from  by swapping two adjacent rows. Furthermore, let
by swapping two adjacent rows. Furthermore, let 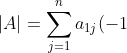^{1+j}m_{1j}^A) and
and 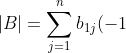^{1+j}m_{1j}^B) . Clearly,
. Clearly,
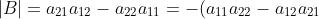=-\vert A\vert)
Let’s assume that for 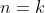 ,
,  when two adjacent rows are swapped. For
when two adjacent rows are swapped. For 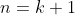 , we have:
, we have:
Case 1: Suppose that the first row of  is not swapped when making
is not swapped when making 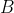 .
.
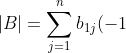^{1+j}M_{1j}^B=\sum_{j=1}^na_{1j}(-1)^{1+j}M_{1j}^B)
 is the determinant of a rank
is the determinant of a rank 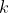 matrix, which is the same as
matrix, which is the same as  except for two adjacent rows being swapped. Therefore,
except for two adjacent rows being swapped. Therefore,  and
and 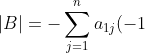^{1+j}M_{1j}^A=-\vert A\vert) .
.
Case 2: If the first two rows of  are swapped when making
are swapped when making 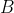 ,
,

We have 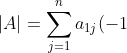^{1+j}M_{1j}^A) and
and 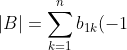^{1+k}M_{1k}^B=\sum_{k=1}^na_{2k}(-1)^{1+k}M_{1k}^B) . The minors
. The minors  and
and  can be expressed as
can be expressed as
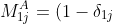\sum_{k=1}^{j-1}a_{2k}(-1)^{1+k}\vert A_{kj}\vert+\sum_{k=j+1}^na_{2k}(-1)^{k}\vert A_{jk}\vert)
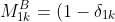\sum_{j=1}^{k-1}a_{1j}(-1)^{1+j}\vert A_{jk}\vert+\sum_{j=k+1}^na_{1j}(-1)^{j}\vert A_{kj}\vert)
where  is
is  with the first two rows, and the
with the first two rows, and the 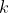 -th and
-th and 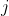 -th columns removed.
-th columns removed.
Therefore,
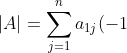^{1+j}\biggr\[(1-\delta_{1j})\sum_{k=1}^{j-1}a_{2k}(-1)^{1+k}\vert A_{kj}\vert+\sum_{k=j+1}^na_{2k}(-1)^{k}\vert A_{jk}\vert\biggr\])
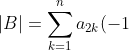^{1+k}\biggr\[(1-\delta_{1k})\sum_{j=1}^{k-1}a_{1j}(-1)^{1+j}\vert A_{jk}\vert+\sum_{j=k+1}^na_{1j}(-1)^{j}\vert A_{kj}\vert\biggr\])
For any pair of values of 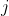 and
and 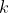 , where
, where  , the terms in
, the terms in  are
are ^{1+j}\sum_{k=1}^{j-1}a_{2k}(-1)^{1+k}\vert A_{kj}\vert) , which differ from the terms in
, which differ from the terms in  , i.e.
, i.e. ^{1+k}\sum_{j=k+1}^{n}a_{1j}(-1)^{j}\vert A_{kj}\vert) , by a factor of -1. Similarly, for any pair of values of
, by a factor of -1. Similarly, for any pair of values of 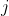 and
and 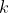 , where
, where  , the terms in
, the terms in  are
are ^{1+j}\sum_{k=j+1}^{n}a_{2k}(-1)^{k}\vert A_{jk}\vert) , which again differ from the terms in
, which again differ from the terms in  , i.e.
, i.e. ^{1+k}\sum_{j=1}^{k-1}a_{1j}(-1)^{1+j}\vert A_{jk}\vert) , by a factor of -1. Since all terms in
, by a factor of -1. Since all terms in  differ from all corresponding terms in
differ from all corresponding terms in  by a factor of -1,
by a factor of -1,  .
.
In general, the swapping of any two rows 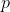 and
and 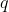 of
of  , where
, where  , is equivalent to the swapping of
, is equivalent to the swapping of -1) adjacent rows of
adjacent rows of  , with each swap changing
, with each swap changing  by a factor of -1. Therefore,
by a factor of -1. Therefore,
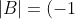^{2(q-p)-1}\vert A\vert=[(-1)^2]^{p-q}(-1)^{-1}\vert A\vert=-\vert A\vert)
Finally, the swapping of any two columns is proven in a similar way.
Proof of property 9
Consider the swapping of two equal rows of  to form
to form 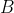 , resulting in
, resulting in  and
and  . However, property 8 states that
. However, property 8 states that  if any two rows of are swapped. Therefore,
if any two rows of are swapped. Therefore,  if two rows of
if two rows of  are equal. The same logic applies to proving
are equal. The same logic applies to proving  if there are two equal columns of
if there are two equal columns of  .
.
Proof of property 10
Case 1: 
If  , then
, then  according to property 13. So,
according to property 13. So,  .
.
Case 2: 
Let’s first consider elementary matrices  . A type I elementary matrix is symmetrical about its diagonal, while a type II elementary matrix has one diagonal element equal to
. A type I elementary matrix is symmetrical about its diagonal, while a type II elementary matrix has one diagonal element equal to 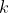 . Therefore,
. Therefore,  and thus
and thus  for type I or II elementary matrices. A type III elementary matrix is an identity matrix with one of the non-diagonal elements replaced by a constant
for type I or II elementary matrices. A type III elementary matrix is an identity matrix with one of the non-diagonal elements replaced by a constant 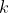 . Therefore, if
. Therefore, if  is a type III elementary matrix, then
is a type III elementary matrix, then  is also one. According to eq6,
is also one. According to eq6,  for a type III elementary matrix. Hence,
for a type III elementary matrix. Hence,  for all elementary matrices.
for all elementary matrices.
Next, consider an invertible matrix  , which (as proven in the previous article) can be expressed as
, which (as proven in the previous article) can be expressed as  . Thus,
. Thus, 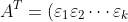^T=\varepsilon_k^T\cdots\varepsilon_2^T\varepsilon_1^T) (see Q&A in the proof of property 13). According to property 5,
(see Q&A in the proof of property 13). According to property 5,

and

Therefore,  .
.
Proof of property 11
We have  , or in terms of matrix components:
, or in terms of matrix components:
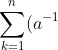_{qk}a_{kp}=\delta_{pq}=\frac{\vert A\vert}{\vert A\vert}\delta_{pq}\;\;\;\;\;\;\;\;7)
Consider the matrix 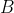 that is obtained from the matrix
that is obtained from the matrix  by replacing the
by replacing the 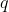 -th column of
-th column of  with the
with the 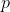 -th column, i.e.
-th column, i.e.  for
for  and
and  . According to property 9,
. According to property 9,  because
because 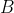 has two equal columns. Furthermore, cofactor
has two equal columns. Furthermore, cofactor  is equal to cofactor
is equal to cofactor  for
for  . Therefore,
. Therefore,

When 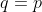 , the last summation in eq8 becomes
, the last summation in eq8 becomes

Combining eq8 and eq9, we have  , which when substituted in eq7 gives:
, which when substituted in eq7 gives:
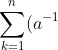_{qk}a_{kp}=\sum_{k=1}^n\frac{A_{kq}}{\vert A\vert}a_{kp})
Therefore, _{qk}=\frac{A_{kq}}{\vert A\vert}) , which implies that the inverse of a matrix is undefined if
, which implies that the inverse of a matrix is undefined if  . In other words, the inverse of a matrix
. In other words, the inverse of a matrix  is undefined if
is undefined if  . We call such a matrix, a singular matrix, and a matrix with an associated inverse, a non-singular matrix.
. We call such a matrix, a singular matrix, and a matrix with an associated inverse, a non-singular matrix.
Proof of property 12
We shall prove by contradiction. According to property 11,  has no inverse if
has no inverse if  . If
. If  has no inverse and
has no inverse and 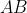 has an inverse, then
has an inverse, then ^{-1}\]=I) . This implies that
. This implies that  has an inverse
has an inverse 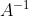 , where
, where 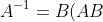^{-1}) , which contradicts the initial assumption that
, which contradicts the initial assumption that  has no inverse. Therefore, if
has no inverse. Therefore, if  has no inverse, then
has no inverse, then 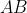 must also have no inverse.
must also have no inverse.
Proof of property 13

Question
Show that ^T=\cdots C^TB^TA^T) .
.
Answer
^T=B^TA^T) because
because
^T_{ij}=(AB)_{ji}=\sum_{k=1}^na_{jk}b_{ki}=\sum_{k=1}^n(A^T)_{kj}(B^T)_{ik}\\=\sum_{k=1}^n(B^T)_{ik}(A^T)_{kj}=(B^TA^T)_{ij})
^T=C^TB^TA^T) because
because
^T_{ij}=(ABC)_{ji}=\sum_{l=1}^n\sum_{k=1}^na_{jk}b_{kl}c_{li}=\sum_{l=1}^n\sum_{k=1}^n(A^T)_{kj}(B^T)_{lk}(C^T)_{il}\\=\sum_{l=1}^n\sum_{k=1}^n(C^T)_{il}(B^T)_{lk}(A^T)_{kj}=(C^TB^TA^T)_{ij})
which can be extended to ^T=\cdots C^TB^TA^T) .
.
Using the identity in the above Q&A, ^TA^T=(AA^{-1})^T) . If
. If  is invertible, then
is invertible, then ^TA^T=(AA^{-1})^T=I=(A^{-1}A)^T=A^T(A^{-1})^T) . This implies that
. This implies that ^T) is the inverse of
is the inverse of  and therefore that
and therefore that  is invertible if
is invertible if  is invertible.
is invertible.
The last part shall be proven by contradiction. Suppose  is singular and
is singular and  is non-singular, there would be a matrix
is non-singular, there would be a matrix 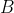 such that
such that  , Furthermore,
, Furthermore, 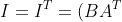^T=AB^T) , which implies that
, which implies that  . This contradicts our initial assumption that
. This contradicts our initial assumption that  is singular. Therefore, if
is singular. Therefore, if  is singular,
is singular,  must also be singular.
must also be singular.
Proof of property 14
We shall proof this property by induction. For 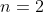 ,
,

Let’s assume that  for
for 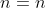 . Then for
. Then for 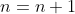 , the cofactor expansion along the first row is
, the cofactor expansion along the first row is

that are conjugate to one another. Two elements
are conjugate to each other if
, where
. If
is conjugate to
, then
is conjugate to
because
(note that
according to the inverse property of a group).
is a class by itself since
.
are represented by matrices,
is called a similarity transformation. Furthermore, if
and
are conjugate to each other, and
and
are conjugate to each other, then
and
are conjugate to each other. This is because
and
and therefore,
, where
.

,
and
of the
point group belong to the same class.
multiplication table,
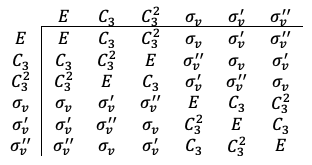
. Since
and
are conjugate to each other, and
and
are conjugate to each other, then
and
are conjugate to each other. Therefore,
form a class. Using the same logic, we find that
and
form another class.
have the same order, which is defined as the smallest value of
such that
, where
. This is because if
is conjugate to
, we have
is valid if and only if
. This means that the smallest value of
in
and in
must be the same. Therefore, elements
and
of the same class in a group have the same order and is denoted by
.

,
and
of the
point group have the same order of 2.
acts on a shape twice, it sends the shape into itself. The same goes for
and
. Hence,
.
to a matrix
leaves the trace of
, which is defined as
, invariant. This implies that elements of the same class in a group have the same trace.