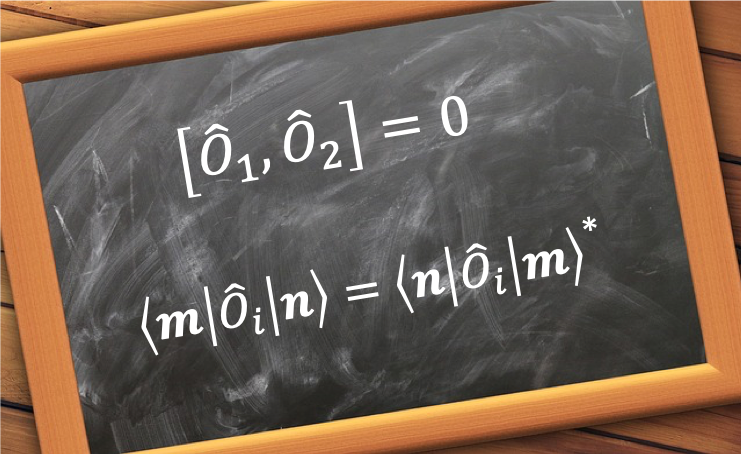Category: Advanced Chemistry

Posted on

Linear combination of wavefunctions

A linear combination of wavefunctions is the weighted sum of a complete set of basis wavefunctions \phi_n.

It is commonly used as a technique in quantum chemistry to approximate a multi-electron wavefunction \psi, where

\psi=\sum_{n=0}^{\infty}c_n\phi_n

Because the Hamiltonian operator \hat{H}=-\frac{\hbar^{2}}{2m}\frac{d^{2}}{dx}+V(x) is a linear operator, a linear combination of \phi_n is a solution to \hat{H} if \{\phi_n\} are solutions to \hat{H}. However, it is only meaningful to solve the eigenvalue equation \hat{H}\psi=E\psi, not just finding solutions to \hat{H}. The problem is \psi (e.g. \psi=c_1\phi_1+c_2\phi_2) is not an eigenfunction of \hat{H}:

\hat{H}(c_1\phi_1+c_2\phi_2)=c_1\hat{H}\phi_1+c_2\hat{H}\phi_2=c_1E_1\phi_1+c_2E_2\phi_2\neq E\psi\; \; \; \; \; \; \; \; 42

The terms on the RHS of the 2nd equality of the above equation cannot be expressed as E\psi, which implies that a state described by \psi does not have a well-defined eigenvalue. Nevertheless, we can find the average value (or expectation value) of \psi. This means that for wavefunctions that are not eigenfunctions of \hat{H}, we can use approximations like \langle H\rangle to find E. The exception to eq42 is if all the basis functions describe a degenerate eigenstate, where E_1=E_2=E:

\hat{H}(c_1\phi_1+c_2\phi_2)=c_1E\phi_1+c_2E\phi_2= E(c_1\phi_1+c_2\phi_2)

In general, a linear combination of wavefunctions (or a linear combination of atomic orbitals, LCAO) is a method of finding an easy or solvable solution to an otherwise complicated or unsolvable one. LCAO is often used in:

    1. Finding the energy of a system using the Hartree-Fock-Roothan method.
    2. Eliminating complex wave functions to find the formula of hydrogenic p/d/f-orbitals that describe their corresponding p/d/f degenerate states.
    3. Constructing wavefunctions that satisfy Pauli’s exclusion principle.
    4. Explaining the relationship between symmetry and degeneracy in group theory.
    5. Constructing symmetry-adapted linear combinations (SALCs) of orbitals, which are building blocks of a molecular orbital (MO) of a molecule.
Next article: postulates of quantum mechanics
Previous article: eigenfunctions and eigenvalue equations
Content page of quantum mechanics
Content page of advanced chemistry
Main content page
Posted on

Eigenfunctions and eigenvalue equations

An eigenfunction in a vector space of function is a non-zero function, f, that when acted upon by an operator \hat{O}, returns the same function but multiplied by a constant c, which is known as an eigenvalue.

\hat{O}f=cf

The above equation is called an eigenvalue equation. The time-independent Schrodinger equation

\hat{H}\psi=E\psi\; \; \; \; \; \; \; \; 40

where \hat{H} is a Hermitian operator called the Hamiltonian, is an example of an eigenvalue equation. We say that the eigenfunction \psi of a stationary state is a solution to the Schrodinger equation. For a one-dimensional, one-particle system in a stationary state, \hat{H}=-\frac{\hbar^{2}}{2m}\frac{d^{2}}{dx^{2}}+V(x), and

\left [-\frac{\hbar^{2}}{2m}\frac{d^{2}}{dx^{2}}+V(x)\right ]\psi=E\psi\; \; \; \; \; \; \; \; 41

where V(x)=\frac{Ze^{2}}{4\pi\varepsilon _0x}.

 

Question

Show that an eigenfunction representing a stationary state satisfies eq40.

Answer

Stationary states of \hat{H} are determinate states, meaning a measurement of the energy of a particle in that state results in the same value of E. Hence, the variance \sigma^{2} of the observable of \hat{H} for a stationary state would be zero, i.e. \sigma^{2}=\frac{\sum_{i=1}^{N}(x_i-\mu)^{2}}{N}=0. Since \frac{\sum_{i=1}^{N}(x_i-\mu)^{2}}{N} is also the average value of (x_i-\mu)^{2},

\sigma^{2}=\langle(H-\langle H\rangle)^{2}\rangle=\langle(H-E)^{2}\rangle=0

where H is the observable of \hat{H} and \langle H\rangle=\langle\psi\vert\hat{H}\vert\psi\rangle denotes the average value of \hat{H}, which is E since \psi is a stationary state of \hat{H}.

Next, we assume that the operator for the observable (H-E)^{2} is (\hat{H}-E)^{2}. Our assumption is only valid if (\hat{H}-E)^{2} is Hermitian, because for any observable in quantum mechanics, there is a corresponding linear, Hermitian operator. This assumption can be verified as follows:

\langle(H-E)^{2}\rangle=\langle\psi\vert(\hat{H}-E)^{2}\vert\psi\rangle=\int \psi^{*}(\hat{H}-E) ^{2}\psi d\tau

\small =\int \psi^{*}(\hat{H}-E)[(\hat{H}-E)\psi]\, d\tau=\int \psi^{*}\hat{H}[(\hat{H}-E)\psi]\, d\tau-\int \psi^{*}E[(\hat{H}-E)\psi]\, d\tau

Using the property of the Hermitian operator \hat{H} and the condition that E is real (E=E^{*}),

\langle(H-E)^{2}\rangle=\int \psi\{\hat{H}[(\hat{H}-E)\psi]\} ^{*}d\tau-\int \psi\{E[(\hat{H}-E)\psi]\} ^{*}d\tau

=\int \psi\{(\hat{H}-E) [(\hat{H}-E)\psi]\}^{*} d\tau=\int \psi[(\hat{H}-E)]^{2}\psi]^{*}\, d\tau

Since , is a Hermitian operator. So,

\langle(H-E)^{2}\rangle=\langle\psi\vert(\hat{H}-E)^{2}\vert\psi\rangle=\langle\psi\vert(\hat{H}-E)[(\hat{H}-E)\psi]\rangle =0

Because (\hat{H}-E)\psi produces another ket, the property of a Hermitian operator gives

\langle\psi\vert(\hat{H}-E)[(\hat{H}-E)\psi]\rangle =\langle[\hat{H}-E)\psi]\vert[(\hat{H}-E)\psi]\rangle ^{*}=0

From the positive semi-definiteness property of the inner product space, where \langle f\vert f\rangle \geq 0, with \langle f\vert f\rangle = 0 if f=0,

\hat{H}\psi=E\psi

 

Examples of functions that are eigenfunctions of \hat{H} are \psi=sinx and \psi=e^{-kx}, and examples of functions that are not eigenfunctions of \hat{H} are \psi=sin(ax)+sin(bx) and \psi=e^{-k_1x}+e^{-k_2x}. We can easily verify whether a function is an eigenfunction or not one by substituting it into eq41.

 

Question

Why is an eigenfunction defined as a non-zero function?

Answer

Since \hat{H}0=E0=0, an eigenfunction that is zero would have an infinite number of eigenvalues (any value of E multiplied by zero is zero), which contradicts the Born interpretation that an acceptable eigenfunction representing a stationary state in quantum mechanics must be single-valued.

 

 

Next article: linear combination of wavefunctions
Previous article: hermitian operator
Content page of quantum mechanics
Content page of advanced chemistry
Main content page
Posted on

Hermitian operator

An operator with domain D_{\hat{O}} is Hermitian if

\langle\boldsymbol{\mathit{m}}\vert\hat{O}\vert\boldsymbol{\mathit{n}}\rangle=\langle\boldsymbol{\mathit{n}}\vert\hat{O}\vert\boldsymbol{\mathit{m}}\rangle^{*}\; \; \; \; \; \; \; \; 35

for all \boldsymbol{\mathit{m}},\boldsymbol{\mathit{n}}\in D_{\hat{O}}.

Eq35 can also be expressed as \langle f_m\vert\hat{O}\vert f_n\rangle=\langle\hat{O}f_m\vert f_n\rangle because

\langle f_m\vert\hat{O}\vert f_n\rangle=\int f_{m}^{*}\hat{O}f_n\: d\tau =\int f_n(\hat{O}f_{m})^{*}\: d\tau=\langle\hat{O}f_m\vert f_n\rangle\; \; \; \; \; \; \; \; 36

where we have used the Hermitian property of the operator in the 2nd equality.

Another way of defining a Hermitian operator is by noting that the average value of a physical property \langle O\rangle must be a real number, i.e. \langle O\rangle=\langle O\rangle^{*} or

\int \psi^{*}\hat{O}\psi\, d\tau =\left ( \int \psi^{*}\hat{O}\psi\: d\tau\right )^{*}=\int \psi(\hat{O}\psi)^{*}d\tau=\int(\hat{O}\psi)^{*}\psi\, d\tau= \langle\hat{O}\psi\vert\psi\rangle\; \; \; \; \; \; \; \; 37

 

Question

Show that eq37 is equivalent to eq36.

Answer

Substitute \psi=f_m+af_n where a is a constant in \int \psi^{*}\hat{O}\psi\, d\tau=\int \psi(\hat{O}\psi)^{*}\, d\tau of eq37 and simplify to give:

a^{*}\int f_{n}^{*}\hat{O}f_m\: d\tau+a\int f_{m}^{*}\hat{O}f_n\: d\tau=a\int f_n(\hat{O}f_{m})^{*}\: d\tau+a^{*}\int f_m(\hat{O}f_{n})^{*}\: d\tau\; \; \; \; \; \; \; \; 38

Since \psi can be expressed as any linear combination of the basis functions f_m and f_n, a can be any number. If we carry out the following:

  1. Substitute a=1 in eq38
  2. Subsitute a=i in eq38 and divide the resultant equation by i
  3. Sum the two resultant equations

we have eq36.

 

Hermitian operators have the following properties:

    1. Eigenfunctions of a Hermitian operator form a complete set
    2. Eigenvalues of a Hermitian operator are real
    3. Eigenfunctions of a Hermitian operator are orthogonal (if they have distinct eigenvalues) or can be chosen to be orthogonal (if they describe a degenerate state)

The first property is a postulate of quantum mechanics. For the 2nd property, consider two eigenvalue equations \hat{O}f_m=a_mf_m and \hat{O}f_n=a_nf_n. Multiplying the first equation on the left by f_{n}^{*}, multiplying the complex conjugate of the 2nd equation on the left by f_m, and then subtracting the two resultant equations and rearranging, yields:

f_{n}^{*}\hat{O}f_m-f_m\hat{O}^{*}f_{n}^{*}=(a_m-a_{n}^{*})f_{n}^{*}f_m

\int f_{n}^{*}\hat{O}f_m\, d\tau-\int f_m\hat{O}^{*}f_{n}^{*}\, d\tau=(a_m-a_{n}^{*})\int f_{n}^{*}f_m \, d\tau

Using the 2nd equality of eq36,

(a_m-a_{n}^{*})\int f_{n}^{*}f_m \, d\tau=0\; \; \; \; \; \; \; \; 39

To show that eigenvalues of a Hermitian operator are real, let m=n

(a_n-a_{n}^{*})\int \vert f_{n}\vert^{2}\, d\tau=0

The integral is zero if and only if f_n were zero over its entire domain. However, an eigenfunction is defined as a non-zero function. Therefore, a_n=a_{n}^{*}.

For the 3rd property, we rewrite eq39 as

(a_m-a_{n})\int f_{n}^{*}f_m \, d\tau=0

If m\neq n, we have a_m-a_n\neq 0 and so, \int f_{n}^{*}f_m\, d\tau=0.

Examples of Hermitian operators are \hat{x} and \hat{p}.

 

Question

Show that \hat{x} and \hat{p}_x are Hermitian.

Answer

We need to show that \int \psi^{*}\hat{O}\psi\, d\tau=\left ( \int \psi^{*}\hat{O}\psi\, d\tau\right )^{*}.

For \hat{x}, we have

\int \psi^{*}\hat{x}\psi\, d\tau=\int \psi^{*}x\psi\, d\tau=\int \psi x\psi^{*} \, d\tau=\left ( \int \psi^{*}x\psi\, d\tau\right )^{*}=\left ( \int \psi^{*}\hat{x}\psi\, d\tau\right )^{*}

where, for the 3rd equality, we used the fact that x is the position of a particle which must be real (x^{*}=x).

For \hat{p}_x, we integrate \int_{-\infty}^{\infty}\psi^{*}(x)\frac{\hbar}{i}\frac{d}{dx}\psi(x)dx by parts to give:

\int_{-\infty}^{\infty}\psi^{*}(x)\frac{\hbar}{i}\frac{d}{dx}\psi(x)dx=\left [\frac{\hbar}{i}\psi^{*}(x)\psi(x)\right ]_{-\infty}^{\infty}+\int_{-\infty}^{\infty}\psi(x)\left (- \frac{\hbar}{i}\right )\frac{d}{dx}\psi^{*}(x)dx

Since a well-behaved wavefunction that is square-integrable is defined as \int_{-\infty}^{\infty}\left | \psi(x)\right |^{2}dx< \infty, i.e. it vanishes at x=\pm \infty, the 1st term on the RHS of the above equation vanishes and we have:

\int_{-\infty}^{\infty}\psi^{*}(x)\frac{\hbar}{i}\frac{d}{dx}\psi(x)dx=\int_{-\infty}^{\infty}\psi(x)\left (- \frac{\hbar}{i}\right )\frac{d}{dx}\psi^{*}(x)dx=\left [ \int_{-\infty}^{\infty}\psi^{*}(x)\frac{\hbar}{i}\frac{d}{dx}\psi(x)dx\right ]^{*}

 

Finally, two operators \hat{A} and \hat{B} are defined as a Hermitian conjugate pair if

\langle\boldsymbol{\mathit{m}}\vert\hat{A}\vert\boldsymbol{\mathit{n}}\rangle=\langle\boldsymbol{\mathit{n}}\vert\hat{B}\vert\boldsymbol{\mathit{m}}\rangle^{*}

 

 

Next article: eigenfunctions and eigenvalue equations
Previous article: expectation value
Content page of quantum mechanics
Content page of advanced chemistry
Main content page
Posted on

Expectation value (quantum mechanics)

The expectation value of a quantum-mechanical operator \hat{O} is the weighted average value of its observable. It is defined as:

\langle O\rangle=\langle\psi\vert\hat{O}\vert\psi\rangle\; \; \; \; \; \; \; \; \; \; \; 34

The above equation has roots in probability theory, where the expectation value or expected value of an observable O is \langle O\rangle=\sum_{i=1}^{N}p_io_i, with p_i being the probability of observing the outcome o_i.

\langle O\rangle=\sum_{i=1}^{N}p_io_i=\sum_{i=1}^{N}\left | \langle\phi_i\vert\psi \rangle\right |^{2}o_i=\sum_{i=1}^{N} \langle\phi_i\vert\psi \rangle^{*}\langle\phi_i\vert\psi \rangle o_i

=\sum_{i=1}^{N} \langle\psi\vert\phi_i \rangle\langle\phi_i\vert\psi \rangle o_i=\langle\psi\vert\biggr\(\sum_{i=1}^{N}o_i\vert\phi_i \rangle\langle\phi_i\biggr\)\vert\psi \rangle

From eq30, \hat{O}=\sum_{i=1}^{N}o_i\vert\phi_i \rangle\langle\phi_i\vert, and so

\langle O\rangle=\langle\psi\vert\hat{O}\vert\psi \rangle

We further postulate that eq34 is valid for an infinite dimensional Hilbert space.

 

Question

Why is p_i=\vert\langle\phi_i\vert\psi\rangle\vert^{2} ?

Answer

Consider an operator with a complete set of orthonormal basis eigenfunctions \left \{ \phi_i \right \}. So, any eigenfunction \psi can be written as a linear combination of these basis eigenfunctions, i.e. \psi=\sum_{i=1}^{N}c_i\phi_i. According to the Born rule, the probability that a measurement will yield a given result is \vert\psi\vert^{2}=\psi^{*}\psi, where \int\psi^{*}\psi\: d \tau=1. So,

\int\psi^{*}\psi\: d \tau=\int \sum_{i=1}^{N}c_{i}^{*}\phi_{i}^{*}\sum_{i=1}^{N}c_{i}\phi_{i}d\tau=\sum_{i=1}^{N}\vert c_{i}\vert^{2}\int \phi_{i}^{*}\phi_i d\tau=\sum_{i=1}^{N}\vert c_{i}\vert^{2}=1

We have used the orthonormal property of  in the 2nd and 3rd equalities. \vert c_i\vert^2 is interpreted as the probability that a measurement of a system will yield an eigenvalue associated with the eigenfunction . Therefore,

\vert\langle\phi_i\vert\psi\rangle\vert^{2}=\vert\langle\phi_i\vert\sum_j c_j\phi_j\rangle\vert^{2}=\vert\langle\phi_i\vert\ c_i\phi_i\rangle\vert^{2}=\vert c_i\vert^{2}

 

Question

Using the Schrodinger equation, show that the expectation value of the Hamiltonian is E=\int \psi_i^{*}\hat{H}\psi_i\: d\tau.

Answer

Multiplying both sides of eq40 on the left by \psi_i^{*} and integrating over all space, we have

E=\frac{\int \psi_i^{*}\hat{H}\psi_i\: d\tau}{\int \psi_i^{*}\psi_i\: d\tau}

If the wavefunction is normalised, the above equation becomes E=\int \psi_i^{*}\hat{H}\psi_i\: d\tau.

 

 

Next article: hermitian operator
Previous article: projection operator
Content page of quantum mechanics
Content page of advanced chemistry
Main content page
Posted on

Projection operator (quantum mechanics)

A projection operator \hat{P} is a linear operator that transforms a vector in the direction of another vector, i.e., it projects one vector onto another.

In general,

\hat{P}=\vert\boldsymbol{\mathit{u}}\rangle\langle\boldsymbol{\mathit{v}}\vert

\hat{P}\vert\boldsymbol{\mathit{w}}\rangle=(\vert\boldsymbol{\mathit{u}}\rangle\langle\boldsymbol{\mathit{v}}\vert)\vert\boldsymbol{\mathit{w}}\rangle=\vert\boldsymbol{\mathit{u}}\rangle(\langle\boldsymbol{\mathit{v}}\vert\boldsymbol{\mathit{w}}\rangle) =c\vert\boldsymbol{\mathit{u}}\rangle

where c is a scalar.

It is useful in quantum mechanics to have a projection operator that maps a vector onto another vector, which is part of a complete set of orthonormal basis vectors \left \{\boldsymbol{\mathit{i}} \right \} in a Hilbert space. We define the operator as:

\hat{P}_{\boldsymbol{\mathit{i}=\boldsymbol{\mathit{m}}}}=\vert\boldsymbol{\mathit{m}}\rangle\langle\boldsymbol{\mathit{m}}\vert

This allows us to project a vector \boldsymbol{\mathit{w}} onto the basis vector \boldsymbol{\mathit{m}}:

\hat{P}_{\boldsymbol{\mathit{i}=\boldsymbol{\mathit{m}}}}\vert\boldsymbol{\mathit{w}}\rangle=\vert\boldsymbol{\mathit{m}}\rangle\langle\boldsymbol{\mathit{m}}\vert\boldsymbol{\mathit{w}}\rangle=c\vert\boldsymbol{\mathit{m}}\rangle

If \boldsymbol{\mathit{w}} is a wavefunction \psi that is a linear combination of a complete set of orthonormal basis functions, i.e., \psi=\sum_{i=1}^{N}c_i\phi_i, then

\hat{P}_i\psi=\vert\phi_i\rangle\langle\phi_i\vert\psi\rangle=c_i\phi_i

When we measure an observable of a system whose state is described by \psi, we get an eigenvalue corresponding to an eigenfunction, which is one of the orthonormal basis functions in the complete set. We say that the wavefunction \psi is projected onto (or collapsed into) the eigenfunction \phi_i.

 

 

Next article: expectation value
Previous article: matrix elements of an operator
Content page of quantum mechanics
Content page of advanced chemistry
Main content page
Posted on

Matrix elements of an operator

The matrix elements of an operator are the entries of the matrix representation of the operator.

Consider a linear map from a vector space \vert\psi\rangle to the same vector space, i.e. \vert\phi\rangle=\hat{O}\vert\psi\rangle, where and the orthonormal basis states \vert\varphi_n\rangle span . The matrix representation of the equation is

\begin{pmatrix} \phi_1\\\phi_2 \\ \vdots \end{pmatrix}=\begin{pmatrix} O_{11} &O_{12} &\cdots \\ O_{21} &O_{22} &\cdots \\ \vdots & \vdots &\ddots \end{pmatrix}\begin{pmatrix} \psi_1\\\psi_2 \\ \vdots \end{pmatrix}

where \phi_m and \psi_n are the coefficients of the vectors \vert\phi\rangle and \vert\psi\rangle respectively.

The matrix elements of \vert\phi\rangle are given by

\phi_m=\sum_{n}O_{mn}\psi_n\; \; \; \; \; \; \; \; 32a

Since the orthonormal basis states \vert\varphi_n\rangle span , we have . So,

\vert\phi\rangle=\hat{O} \sum_{n}\vert\varphi_n\rangle\langle\varphi_n\vert\psi\rangle =\sum_{n}\hat{O}\vert\varphi_n\rangle\langle\varphi_n\vert\psi\rangle

\langle\varphi_m\vert\phi\rangle=\sum_{n}\langle\varphi_m\vert\hat{O}\vert\varphi_n\rangle\langle\varphi_n\vert\psi\rangle

Similarly, and so

Comparing eq33 with eq32a, O_{mn}=\langle\varphi_m\vert\hat{O}\vert\varphi_n\rangle. Therefore, O_{mn} are the matrix elements of \hat{O} with respect to the basis states of \vert\varphi_n\rangle.

 

Next article: projection operator
Previous article: spectral decomposition of an operator
Content page of quantum mechanics
Content page of advanced chemistry
Main content page
Posted on

Spectral decomposition of an operator

The spectral decomposition (also known as eigendecomposition or diagonalisation) of an operator is the transformation of an operator in a given basis to one in another basis, such that the resultant operator is represented by a diagonal matrix.

There are 2 main reasons for diagonalising an operator, especially a Hermitian operator. One is to find its eigenvalues and the other is to convert it into a form that is easier to multiply with.

 

Question

What is a spectrum with respect to linear algebra?

Answer

A spectrum is a collection of all eigenvalues of a matrix. If the matrix represents an operator, its spectral decomposition transforms it to a diagonal matrix with the eigenvalues as its diagonal elements.

 

Consider an operator with a complete set of orthonormal eigenvectors \{\boldsymbol{\mathit{e_i}}\} that is represented by the eigenvalue equation \hat{O}\vert\boldsymbol{\mathit{e_i}}\rangle=o_i\vert\boldsymbol{\mathit{e_i}}\rangle, where i\in \mathbb{N} and o_i are eigenvalues of \hat{O}. Since the eigenvectors form a complete set, any vector \boldsymbol{\mathit{u}} can be written as a linear combination of the basis eigenvectors:

\vert\boldsymbol{\mathit{u}}\rangle=\sum_{i=1}^{N}c_i\vert\boldsymbol{\mathit{e_i}}\rangle \; \; \; \; \; \; \; \; 28

where c_i is the coefficient of the basis eigenvector.

Letting \hat{O} act on eq28, \hat{O}\vert\boldsymbol{\mathit{u}}\rangle=\sum_{i=1}^{N}c_io_i\vert\boldsymbol{\mathit{e_i}}\rangle. As we have a complete set of orthonormal eigenvectors,  \langle\boldsymbol{\mathit{e_i}}\vert\boldsymbol{\mathit{u}}\rangle=c_i and \hat{O}\vert\boldsymbol{\mathit{u}}\rangle=\sum_{i=1}^{N}\langle\boldsymbol{\mathit{e_i}}\vert\boldsymbol{\mathit{u}}\rangle o_i\vert\boldsymbol{\mathit{e_i}}\rangle. Furthermore, \langle\boldsymbol{\mathit{e_i}}\vert\boldsymbol{\mathit{u}}\rangle is a scalar and matrix multiplication is associative. Therefore,

\hat{O}\vert\boldsymbol{\mathit{u}}\rangle=\sum_{i=1}^{N}o_i\vert\boldsymbol{\mathit{e_i}}\rangle\langle\boldsymbol{\mathit{e_i}}\vert\boldsymbol{\mathit{u}}\rangle =\left\(\sum_{i=1}^{N}o_i\vert\boldsymbol{\mathit{e_i}}\rangle\langle\boldsymbol{\mathit{e_i}}\vert\right\)\vert\boldsymbol{\mathit{u}}\rangle\; \; \; \; \; \; \; \; 29

and

\hat{O}=\sum_{i=1}^{N}o_i\vert\boldsymbol{\mathit{e_i}}\rangle\langle\boldsymbol{\mathit{e_i}}\vert\; \; \; \; \; \; \; \; 30

We call eq30 the spectral decomposition of \hat{O}. Since  is the projection operator onto the eigenspace corresponding to o_i, we can say that the spectral decomposition of a quantum operator represents the operator as a sum of projections onto its eigenstates, weighted by its eigenvalues.

 

Question

Show that \hat{O} in eq30, where N=3, is represented by a diagonal matrix.

Answer

\hat{O}=o_1 \begin{pmatrix} 1\\ 0\\0 \end{pmatrix} \begin{pmatrix} 1 &0 &0 \end{pmatrix}+o_2 \begin{pmatrix} 0\\ 1\\0 \end{pmatrix} \begin{pmatrix} 0 &1 &0 \end{pmatrix}+o_3 \begin{pmatrix} 0\\ 0\\1 \end{pmatrix} \begin{pmatrix} 0 &0 &1 \end{pmatrix}

\hat{O}=o_1 \begin{pmatrix} 1 &0 &0 \\ 0 &0 &0 \\ 0 &0 &0 \end{pmatrix}+o_2 \begin{pmatrix} 0 &0 &0 \\ 0 &1 &0 \\ 0 &0 &0 \end{pmatrix}+o_3 \begin{pmatrix} 0 &0 &0 \\ 0 &0 &0 \\ 0 &0 &1 \end{pmatrix}=\begin{pmatrix} o_1 &0 &0 \\ 0 &o_2 &0 \\ 0 &0 &o_3 \end{pmatrix}

Each o_i is a diagonal element of the operator, as well as an eigenvalue of the operator.

 

In other words, any operator can be expressed in the form of a diagonal matrix if it has the following properties:

    1. Eigenvectors of the operator form a complete set, i.e. the eigenvectors span the vector space.
    2. Eigenvectors of the operator are orthogonal or can be chosen to be orthogonal.

If the eigenvalues of \hat{O} are real,

This implies that a Hermitian operator can also be expressed in the form of a diagonal matrix because the properties of a Hermitian matrix are:

    1. Eigenvectors of the operator form a complete set, i.e. the eigenvectors span the vector space.
    2. Eigenvectors of the operator are orthogonal or can be chosen to be orthogonal.
    3. Eigenvalues of the operator are real.
    4. \hat{O}.

 

 

Next article: matrix elements of an operator
Previous article: the energy-time uncertainty relation
Content page of quantum mechanics
Content page of advanced chemistry
Main content page
Posted on

The uncertainty principle (derivation)

Heisenberg’s uncertainty principle states that the position and momentum of a particle cannot be determined simultaneously with unlimited precision.

The uncertainty not only applies to the position and momentum of a particle, but to any pair of complementary observables, e.g. energy and time. In general, the uncertainty principle is expressed as:

\Delta A\Delta B\geq \frac{1}{2}\left\vert\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle\right\vert\; \; \; \; \; \; \; \; \; 12

where \hat{A} and \hat{B} are Hermitian operators and A and B are their respective observables.

The derivation of eq12 involves the following:

  1. Deriving the Schwarz inequality
  2. Proving the inequality \left ( \Delta A \right )^{2}\left ( \Delta B \right )^{2}\geq -\frac{1}{4}\left ( \left \langle \varphi \left | \left [ \hat{A},\hat{B} \right ] \right |\varphi \right \rangle \right )^{2}
  3. Showing that \left \langle \varphi \left | \left [ \hat{A},\hat{B} \right ] \right |\varphi \right \rangle =-\left \langle \varphi \left | \left [ \hat{A},\hat{B} \right ] \right |\varphi \right \rangle^{*}

 

Step 1

Let

f(\lambda)=\langle\phi-\lambda\psi\vert\phi-\lambda\psi\rangle\; \; \; \; \; \; \; \; 13

where \phi and \psi are arbitrary square integrable wavefunctions and \lambda is an arbitrary scalar.

Since \langle\phi-\lambda\psi\vert\phi-\lambda\psi\rangle=\int (\phi-\lambda\psi)^{*}(\phi-\lambda\psi)d\tau=\int \vert\phi-\lambda\psi\vert^{2}d\tau\geq 0

f(\lambda)\geq 0\; \; \; \; \; \; \; \; \; 14

Expanding eq13, we have

f(\lambda)=\langle\phi\vert\phi\rangle-\lambda\langle\phi\vert\psi\rangle-\lambda^{*}\langle\psi\vert\phi\rangle+\lambda^{*}\lambda\langle\psi\vert\psi\rangle\; \; \; \; \; \; \; \; 15

Since \lambda is an arbitrary scalar, substituting \lambda=\frac{\langle\psi\vert\phi\rangle}{\langle\psi\vert\psi\rangle} and \lambda^{*}=\frac{\langle\phi\vert\psi\rangle}{\langle\psi\vert\psi\rangle} in eq15 gives:

f(\lambda)=\langle\phi\vert\phi\rangle-\frac{\langle\phi\vert\psi\rangle}{\langle\psi\vert\psi\rangle}\langle\psi\vert\phi\rangle

Substituting eq14 in the above equation and rearranging yields \langle\phi\vert\psi\rangle\langle\psi\vert\phi\rangle \leq\langle\phi\vert\phi\rangle\langle\psi\vert\psi\rangle. Since \langle\phi\vert\psi\rangle= \langle\psi\vert\phi\rangle^{*}

\vert\langle\psi\vert\phi\rangle\vert^{2}\leq\langle\phi\vert\phi\rangle\langle\psi\vert\psi\rangle\; \; \; \; \; \; \; \; 16

Eq16 is called the Schwarz Inequality.

 

Step 2

Let \psi=(\hat{A}-\langle A\rangle)\varphi and \phi=(\hat{B}-\langle B\rangle)\varphi, where \varphi is normalised, and \hat{A} and \hat{B} are Hermitian operators, which implies that \hat{A}-\langle A\rangle and \hat{B}-\langle B\rangle are also Hermitian operators (see this article for proof). The variance of the observable of \hat{A} is

(\Delta A)^{2}=\frac{\sum_{i=1}^{N}(\hat{A}-\langle A\rangle)^{2}}{N}=\langle(\hat{A}-\langle A\rangle)^{2} \rangle

=\langle \varphi\vert(\hat{A}-\langle A\rangle)[(\hat{A}-\langle A\rangle)\varphi]\rangle=\langle [(\hat{A}-\langle A\rangle)\varphi]\vert[(\hat{A}-\langle A\rangle)\varphi]\rangle=\langle\psi\vert\psi \rangle\; \; \; \; \; \; \; \; 17

Note that the 2nd last equality uses the property of Hermitian operators (see eq36). Similarly,

(\Delta B)^{2}=\langle\phi\vert\phi\rangle\; \; \; \; \; \; \; \; 18

Substituting eq17 and eq18 in eq16 results in

(\Delta A)^{2}(\Delta B)^{2} \geq\vert \langle\psi\vert\phi\rangle\vert^{2} \; \; \; \; \; \; \; \; 19

Let z= \langle\psi\vert\phi\rangle where z=x+iy. So, \left | z \right |^{2}=x^{2}+y^{2}\geq y^{2}. Since y=\frac{z-z^{*}}{2i}, we have \left | z \right |^{2}\geq \left ( \frac{z-z^{*}}{2i} \right )^{2}, which is

\left | \langle\psi\vert\phi\rangle\right |^{2}\geq \left ( \frac{\langle\psi\vert\phi\rangle-\langle\psi\vert\phi\rangle^{*}}{2i} \right )^{2}=-\frac{1}{4}\left (\langle\psi\vert\phi\rangle-\langle\phi\vert\psi\rangle\right )^{2}\; \; \; \;\; \; \; \; 20

Substituting eq19 in eq20 gives

(\Delta A)^{2}(\Delta B)^{2}\geq -\frac{1}{4}\left ( \langle\psi\vert\phi\rangle-\langle\phi\vert\psi\rangle\right )^{2}\; \; \; \; \; \; \; \; 21

Next, we have

\langle\psi\vert\phi\rangle= \langle (\hat{A}-\langle A\rangle)\varphi\vert (\hat{B}-\langle B\rangle )\varphi\rangle=\langle\varphi\vert(\hat{A}-\langle A\rangle)(\hat{B}-\langle B\rangle)\varphi\rangle

=\langle\varphi\vert\hat{A}\hat{B}\vert\varphi\rangle-\langle B\rangle\langle\varphi\vert\hat{A}\vert\varphi\rangle-\langle A\rangle\langle\varphi\vert\hat{B}\vert\varphi\rangle+\langle A\rangle\langle B \rangle\langle\varphi\vert\varphi\rangle

=\langle\varphi\vert\hat{A}\hat{B}\vert\varphi\rangle-\langle A\rangle\langle B \rangle \; \; \; \; \; \; \; \; 22

Similarly,

\langle\phi\vert\psi\rangle=\langle\varphi\vert\hat{B}\hat{A}\vert\varphi\rangle-\langle B\rangle\langle A \rangle \; \; \; \; \; \; \; \; 23

Substituting eq22 and eq23 in eq21 yields

(\Delta A)^{2}(\Delta B)^{2}\geq -\frac{1}{4}(\langle\varphi\vert\hat{A}\hat{B}\vert\varphi\rangle-\langle\varphi\vert\hat{B}\hat{A}\vert\varphi\rangle )^{2}

=-\frac{1}{4}(\langle\varphi\vert\hat{A}\hat{B}-\hat{B}\hat{A}\vert\varphi\rangle )^{2}=-\frac{1}{4}(\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle )^{2}\; \; \; \; \; \; \; \; 24

 

Step 3

\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle=\langle\varphi\vert\hat{A}\hat{B}\vert\varphi\rangle-\langle\varphi\vert\hat{B}\hat{A}\vert\varphi\rangle=\langle\hat{A}\varphi\vert\hat{B}\varphi\rangle-\langle\hat{B}\varphi\vert\hat{A}\varphi\rangle

=\langle\varphi\vert\hat{B}(\hat{A}\varphi)\rangle^{*}-\langle\varphi\vert\hat{A}(\hat{B}\varphi)\rangle^{*}=- \{\langle\varphi\vert\hat{A}(\hat{B}\varphi)\rangle^{*}-\langle\varphi\vert\hat{B}(\hat{A}\varphi)\rangle^{*}\}

=-\{\langle\varphi\vert\hat{A}(\hat{B}\varphi)\rangle-\langle\varphi\vert\hat{B}(\hat{A}\varphi)\rangle\}^{*}=-\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle^{*}\; \; \; \; \; \; \; \; 25

We have used eq37 for the 2nd equality and eq35 for the 3rd equality. Substituting eq25 in one of the \langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi)\rangle in eq24 results in

(\Delta A)^{2}(\Delta B)^{2}\geq\frac{1}{4} \{\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle^{*}\}\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle

Therefore,

(\Delta A)^{2}(\Delta B)^{2}\geq \frac{1}{4}\vert\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle\vert^{2}

\Delta A\Delta B\geq \frac{1}{2}\vert\langle\varphi\vert[\hat{A},\hat{B}]\vert\varphi\rangle\vert\; \; \; \; \; \; \; \; 26

which is eq12, the general form of the uncertainty principle.

For, the observable pair of position x and momentum p, we have

\Delta x\Delta p\geq \frac{1}{2}\vert\langle\varphi\vert[\hat{x},\hat{p}]\vert\varphi\rangle\vert

Since [\hat{x},\hat{p}]\varphi=x\frac{\hbar}{i}\frac{d}{dx}\varphi-\frac{\hbar}{i}\frac{d}{dx}(x\varphi)=i\hbar\varphi

\Delta x\Delta p\geq \frac{1}{2}\vert\langle\varphi\vert i\hbar\varphi\rangle\vert=\frac{\hbar}{2}\vert i\vert

\Delta x\Delta p\geq \frac{\hbar}{2}\; \; \; \; \; \; \; \; 27

 

Next article: The energy-time uncertainty relation
Previous article: commuting operators
Content page of quantum mechanics
Content page of advanced chemistry
Main content page
Posted on

Commuting operators

A pair of commuting operators that are Hermitian can have a common complete set of eigenfunctions.

Let \hat{O}_1 and \hat{O}_2 be two different operators, with observables \Omega_1 and \Omega_2 respectively.

\hat{O}_1(\hat{O}_2\psi)=\hat{O}_1(\Omega_2\psi)=\Omega_2\hat{O}_1\psi=\Omega_2\Omega_1\psi

\hat{O}_2(\hat{O}_1\psi)=\hat{O}_2(\Omega_1\psi)=\Omega_1\hat{O}_2\psi=\Omega_1\Omega_2\psi

So, \hat{O}_1(\hat{O}_2\psi)=\hat{O}_2(\hat{O}_1\psi)\; \; \; or\; \; \;\hat{O}_1(\hat{O}_2\psi)-\hat{O}_2(\hat{O}_1\psi)=0. If this is so, we say that the two operators commute. The short notation for \hat{O}_1(\hat{O}_2\psi)-\hat{O}_2(\hat{O}_1\psi) is \left [\hat{O}_1,\hat{O}_2\right ], where in the case of two commuting operators, \left [\hat{O}_1,\hat{O}_2\right ]=0.

When the effect of two operators depends on their order, we say that they do not commute, i.e. \left [\hat{O}_1,\hat{O}_2\right ]\neq 0. If this is the case, we say that the observables \Omega_1 and \Omega_2 are complementary.

One important concept in quantum mechanics is that we can select a common complete set of eigenfunctions for a pair of commuting Hermitian operators. The proof is as follows:

Let \left \{ \vert a_n\rangle \right \} and \left \{ \vert b_n\rangle \right \} be the complete sets of eigenfunctions of \hat{A} and \hat{B} respectively, such that \hat{A}\vert a_n\rangle=a_n\vert a_n\rangle and \hat{B}\vert b_m\rangle=b_m\vert b_m\rangle. If the two operators have a common complete set of eigenfunctions, we can express \vert a_n\rangle as a linear combination of \vert b_m\rangle:

\vert a_n\rangle=\sum_{m=1}^{k}c_{nm}\vert b_m\rangle\; \; \; \; \; \; \; \; 5

For example, the eigenfunction is:

\vert a_1\rangle=c_{11}\vert b_1\rangle+c_{12}\vert b_2\rangle+\cdots+c_{1k}\vert b_k\rangle\; \; \; \; \; \; \; \; 6

Since some of the eigenfunctions \vert b_m\rangle may describe degenerate states (i.e. some \vert b_m\rangle are associated with the same eigenvalue b_i), we can rewrite \vert a_n\rangle as:

\vert a_n\rangle=\sum_{i=1}^{j}\vert(a_n) b_i\rangle\; \; \; \; \; \; \; \; 7

where \vert(a_n) b_i\rangle=\sum_{m=1}^{k}d_{nm}\vert b_m\rangle\delta_{b_i,b_m} and b_i represents distinct eigenvalues of the complete set of eigenfunctions of \hat{B}.

For example, if the linear combination of \vert a_1 \rangle in eq6 has \vert b_1\rangle and \vert b_2\rangle describing the same eigenstate with eigenvalue b_1, and \vert b_4\rangle and \vert b_5\rangle describing another common eigenstate with eigenvalue b_3,

\vert a_1\rangle=\vert(a_1) b_1\rangle+\vert(a_1) b_2\rangle+\vert(a_1) b_3\rangle+\cdots+\vert(a_1) b_j\rangle

where \vert(a_1) b_1\rangle=d_{11}\vert b_1\rangle+d_{12}\vert b_2\rangle, \vert(a_1) b_2\rangle=d_{13}\vert b_3\rangle, \vert(a_1) b_3\rangle=d_{14}\vert b_4\rangle+d_{15}\vert b_5\rangle and so on.

In other words, eq7 is a sum of eigenfunctions with distinct eigenvalues of \hat{B}. Since a linear combination of eigenfunctions describing a degenerate eigenstate is an eigenfunction of \hat{B}, we have

\hat{B}\vert(a_n)b_i\rangle=b_i\vert(a_n)b_i\rangle\; \; \; \; \; \; \; \; 8

i.e. \vert(a_n)b_i\rangle is an eigenfunction of \hat{B}. Furthermore, the set \left \{ \vert(a_n)b_i\rangle \right \} is complete, which is deduced from eq7, where the set \left \{ \vert a_n\rangle \right \} is complete.

From \hat{A}\vert a_n\rangle=a_n\vert a_n\rangle, we have:

(\hat{A}-a_n)\vert a_n\rangle=0

Substituting eq7 in the above equation, we have

(\hat{A}-a_n)\vert a_n\rangle=\sum_{i=1}^{j}(\hat{A}-a_n) \vert (a_n)b_i\rangle=0\; \; \; \; \; \; \; \; 9

By operating on the 1st term of the summation in the above equation with \hat{B}, and using the fact that \hat{A} commute with \hat{B},

\hat{B}(\hat{A}-a_n)\vert (a_n)b_1\rangle=(\hat{A}-a_n)\hat{B} \vert (a_n)b_1\rangle\; \; \; \; \; \; \; \; 10

Substituting eq8, where i=1 in the above equation,

\hat{B}(\hat{A}-a_n)\vert (a_n)b_1\rangle=b_1(\hat{A}-a_n) \vert (a_n)b_1\rangle\; \; \; \; \; \; \; \; 11

Repeating the operation of \hat{B} on the remaining terms of the summation in eq9, we obtain equations similar to eq11 and we can write:

\hat{B}(\hat{A}-a_n)\vert (a_n)b_i\rangle=b_i(\hat{A}-a_n) \vert (a_n)b_i\rangle

i.e. (\hat{A}-a_n)\vert (a_n)b_i\rangle is an eigenfunction of \hat{B} with distinct eigenvalues b_i. Since \hat{B} is Hermitian and (\hat{A}-a_n)\vert (a_n)b_i\rangle are associated with distinct eigenvalues, the eigenfunctions (\hat{A}-a_n)\vert (a_n)b_i\rangle are orthogonal and therefore linearly independent. Consequently, each term in the summation in eq9 must be equal to zero:

(\hat{A}-a_n)\vert (a_n)b_i\rangle=0\; \; \; \Rightarrow \; \; \;\hat{A}\vert (a_n)b_i\rangle=a_n\vert (a_n)b_i\rangle

This implies that \vert (a_n)b_i\rangle, which is a complete set as mentioned earlier, is also an eigenfunction of \hat{A}. Therefore, we can select a common complete set of eigenfunctions \left \{ \vert (a_n)b_i\rangle\right \} for a pair of commuting Hermitian operators. Conversely, if two Hermitian operators do not commute, eq10 is no longer valid and we cannot select a common complete set of eigenfunctions for them.

 

 

Next article: the uncertainty principle
Previous article: operators
Content page of quantum mechanics
Content page of advanced chemistry
Main content page
Posted on

Operators (quantum mechanics)

An operator \hat{O} in a vector space V maps a set of vectors \boldsymbol{\mathit{v}}_i to another set of vectors \boldsymbol{\mathit{v}}_j (or transforms one function into another function), where \boldsymbol{\mathit{v}}_i,\boldsymbol{\mathit{v}}_j\in V. For example, the operator \frac{d^{2}}{dx^{2}} transforms the function f(x) into f^{''}(x):

\frac{d^{2}}{dx^{2}}f(x)=f^{''}(x)

Linear operators have the following properties:

    1. \hat{O}(\boldsymbol{\mathit{u}}+\boldsymbol{\mathit{v}})=\hat{O}\boldsymbol{\mathit{u}}+\hat{O}\boldsymbol{\mathit{v}}
    2. \hat{O}(c\boldsymbol{\mathit{u}})=c\hat{O}\boldsymbol{\mathit{u}}
    3. (\hat{O}_1\hat{O}_2)\boldsymbol{\mathit{u}}=\hat{O}_1(\hat{O}_2\boldsymbol{\mathit{u}})

Two operators commonly encountered in quantum mechanics are the position and linear momentum operators. To construct these operators, we refer to probability theory, where the expectation value of the position x of a particle in a 1-D box of length L is

\langle x\rangle=\int_{0}^{L}xP(x)dx=\int_{0}^{L}x\left |\psi(x) \right |^{2}dx=\int_{0}^{L}\psi(x)\, x\, \psi(x)dx

where P(x) is the probability of observing the particle at a particular position between 0 and L, and \psi(x) is the particle’s wavefunction, which is assumed to be real.

Comparing the above equation with the expression of the expectation value of a quantum-mechanical operator, \hat{x}=x.

One may infer that the linear momentum operator is \hat{p}_x=p_x. However, we must find a form of p_x that is a function of x so that we can compute \int_{0}^{L}\psi(x)p_x\psi(x)dx. If we compare the time-independent Schrodinger equation \left [ -\frac{\hbar^{2}}{2m}\frac{\partial^{2}}{\partial x^{2}}+V(x) \right ]\psi(x)=E\psi(x) with the total energy equation \frac{p_x^{\: 2}}{2m}+V(x)=E, we have \hat{p}_x=\frac{\hbar}{i}\frac{d}{dx}.

To test the validity of \hat{x}=x and \hat{p}_x=\frac{\hbar}{i}\frac{d}{dx}, we compute \langle x\rangle and \langle p_x\rangle using the 1-D box wavefunction of \sqrt\frac{2}{L}sin\frac{n\pi x}{L} and check if the results are reasonable with respect to classical mechanics.

Integrating \langle x\rangle=\frac{2}{L}\int_{0}^{L}xsin^{2}\left ( \frac{n\pi x}{L} \right )dx by parts, we have \langle x\rangle=\frac{L}{2}. In classical mechanics, the particle can be anywhere in the 1-D box with equal probability. Therefore, the average position of \langle x\rangle=\frac{L}{2} is reasonable.

For the linear momentum operator, we have \langle p_x\rangle=\frac{2\hbar}{iL}\int_{0}^{L}sin\left ( \frac{n\pi x}{L} \right )\frac{d}{dx}sin\left ( \frac{n\pi x}{L} \right )dx=0. Since \langle x\rangle=\frac{L}{2}, we expect \langle p_x\rangle=m\frac{d\langle x\rangle}{dt}=0. Therefore, x and \frac{\hbar}{i}\frac{d}{dx} are reasonable assignments of the position and linear momentum operators respectively. In 3-D, the position and linear momentum operators are:

\hat{x}=x\; \; \; \; \;\hat{y}=y\; \; \; \; \;\hat{z}=z

\hat{p}_x=\frac{\hbar}{i}\frac{\partial}{\partial x}\; \; \; \; \;\hat{p}_y=\frac{\hbar}{i}\frac{\partial}{\partial y}\; \; \; \; \;\hat{p}_z=\frac{\hbar}{i}\frac{\partial}{\partial z}\; \; \; \; \;\; \; \; 4

To see the proof that the position and linear momentum operators are Hermitian, read this article.

 

 

Next article: commuting operators
Previous article: kronecker product
Content page of quantum mechanics
Content page of advanced chemistry
Main content page
Mono Quiz