Dirac bra-ket notation

The Dirac bra-ket notation is a concise way to represent objects in a complex vector space $\mathbb{C}^{n}$ .

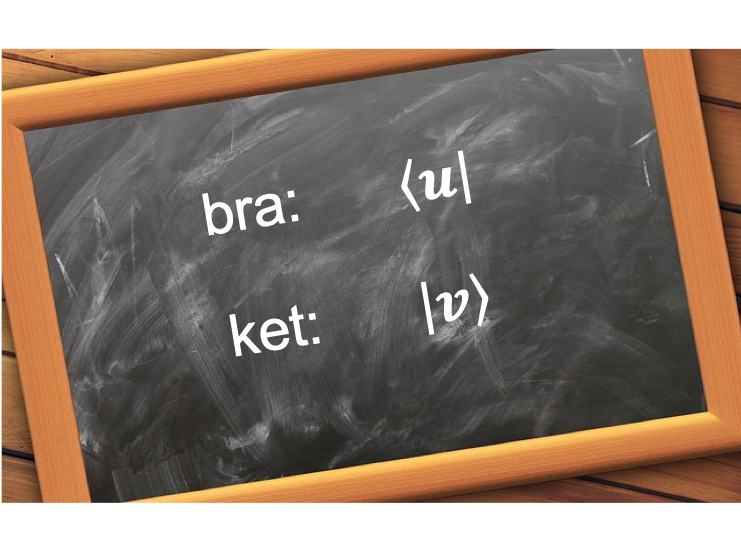
A ket, denoted by $\vert \textbf{v} \rangle$ , is a vector $\textbf{v}$ . Since a linear operator $\hat{O}$ maps a vector to another vector, we have $\hat{O}\vert \boldsymbol{v_{1}}\rangle=\vert \boldsymbol{v_{2}} \rangle$ .

A bra, denoted by $\langle\boldsymbol{u}\vert$ , is often associated with a ket in the form of an inner product, denoted by $\langle\boldsymbol{u}\vert\boldsymbol{v}\rangle$ . If a ket is expressed as a column vector, the corresponding bra is the conjugate transpose of its ket, i.e. $\langle\boldsymbol{u}\vert=\vert\boldsymbol{u}\rangle^{\dagger}$ . The inner product can therefore be written as the following matrix multiplication:

$\langle\boldsymbol{u}\vert\boldsymbol{v}\rangle=\begin{pmatrix} u_{1}^{*}&u_{2}^{*}& \cdots & u_{N}^{*}\end{pmatrix}\begin{pmatrix} v_{1}\\v_{2} \\ \vdots \\v_{N} \end{pmatrix}=\sum_{i=1}^{N}u_{i}^{*}v_i$

or in the case of functions:

$\langle\boldsymbol{u}\vert\boldsymbol{v}\rangle=\int_{-\infty}^{\infty}f_{u}^{*}(x)f_{v}(x)dx$

Since a linear operator acting on a ket is another ket, we can express an inner product as:

$\langle\phi_{i}\vert\phi_{k}\rangle=\langle\phi_{i}\vert\hat{O}\vert\phi_{j}\rangle=\int \phi_{i}^{*}\hat{O}\phi_{j}d\tau$

where $\hat{O}\vert\phi_{j}\rangle=\vert\phi_{k}\rangle$ .

If $i=j$ , then $\langle\phi\vert\hat{O}\vert\phi\rangle$ is the expectation value (or average value) of the operator $\hat{O}$ .

As mentioned above, bras and kets can be represented by matrices. Therefore, the multiplication of a bra and a ket that involves a linear operator is associative, e.g.:

$\langle\boldsymbol{u}\vert(\hat{O}\vert\boldsymbol{v}\rangle)=(\langle\boldsymbol{u}\vert\hat{O})\vert\boldsymbol{v}\rangle\equiv\langle\boldsymbol{u}\vert\hat{O}\vert\boldsymbol{v}\rangle$

$(\vert\boldsymbol{u}\rangle\langle\boldsymbol{v}\vert)\vert\boldsymbol{w}\rangle=\vert\boldsymbol{u}\rangle(\langle\boldsymbol{v}\vert\boldsymbol{w}\rangle)$

$(\hat{O}\vert\boldsymbol{u}\rangle)\langle\boldsymbol{v}\vert=\hat{O}(\vert\boldsymbol{u}\rangle\langle\boldsymbol{v}\vert)\equiv\hat{O}\vert\boldsymbol{u}\rangle\langle\boldsymbol{v}\vert$

You can verify the above examples using a 2×2 matrix with complex elements to represent the operator acting on a vector in $\mathbb{C}^{2}$ . The three examples reveal that:

1. $\hat{O}\vert\boldsymbol{v}\rangle$ produces another ket.
2. $\langle\boldsymbol{u}\vert\hat{O}$ results in another bra. This is because $(\langle\boldsymbol{u}\vert\hat{O})\vert\boldsymbol{v}\rangle=\langle\boldsymbol{u}\vert(\hat{O}\vert\boldsymbol{v}\rangle)=\langle\boldsymbol{u}\vert\boldsymbol{v'}\rangle=c$ , where $c$ is a scalar; and if $(\langle\boldsymbol{u}\vert\hat{O})\vert\boldsymbol{v}\rangle=c$ , the only possible identity of $(\langle\boldsymbol{u}\vert\hat{O})$ is a bra.
3. $\vert\boldsymbol{u}\rangle\langle\boldsymbol{v}\vert$ , which is called an outer product, is an operator because $(\vert\boldsymbol{u}\rangle\langle\boldsymbol{v}\vert)\vert\boldsymbol{w}\rangle=\vert\boldsymbol{u}\rangle(\langle\boldsymbol{v}\vert\boldsymbol{w}\rangle)=c\vert\boldsymbol{u}\rangle$ , i.e. $\vert\boldsymbol{u}\rangle\langle\boldsymbol{v}\vert$ maps the ket $\vert\boldsymbol{w}\rangle$ to another ket $c\vert\boldsymbol{u}\rangle$ . In other words, the operator $\vert\boldsymbol{u}\rangle\langle\boldsymbol{v}\vert$ transforms the vector $\vert\boldsymbol{w}\rangle$ in the direction of the vector $\vert\boldsymbol{u}\rangle$ , i.e. $\vert\boldsymbol{u}\rangle\langle\boldsymbol{v}\vert$ projects $\vert\boldsymbol{w}\rangle$ onto $\vert\boldsymbol{u}\rangle$ .
4. The product of two linear operators is another linear operator: $\hat{O}\hat{O'}=\hat{O}(\vert\boldsymbol{u}\rangle\langle\boldsymbol{v}\vert)=(\hat{O}\vert\boldsymbol{u}\rangle)\langle\boldsymbol{v}\vert=\vert\boldsymbol{u'}\rangle\langle\boldsymbol{v}\vert=\hat{O''}$ .

Dirac bra-ket notation

Next article: vector space

Previous article: stationary state

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply