Electron spin

Electron spin is a fundamental quantum property that describes the intrinsic angular momentum of electrons, significantly influencing their behavior in atomic and molecular systems, as well as in phenomena like magnetism and spectroscopy.

Ever since scientists recorded the first hydrogen emission spectrum, they produced many significant findings, including the Balmer and Lyman series, the Rydberg formula and the Bohr model. However, when researchers scrutinised the spectrum under magnification, they discovered that the emission line from n = 2 to n = 1 consisted of two lines (see diagram below).

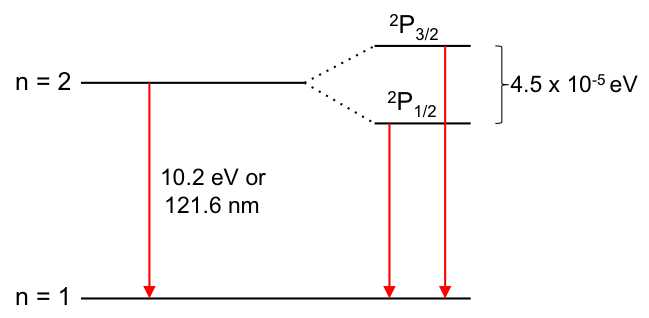
This splitting of emission lines is called the hydrogen fine structure. Many attempts were made to explain this phenomenon without success. At around 1924, Wolfgang Pauli, an Austrian physicist, and two other scientists (George Uhlenbeck and Samuel Goudsmit, both Dutch scientists), separately proposed that an electron possesses an intrinsic property called spin. Although the spin of an electron is purely a quantum mechanical property with no classical analogue, some intuition can be gained by considering classical electromagnetism.

In the classical picture, an electron moving in an orbit around a nucleus constitutes a current loop, which generates a magnetic (orbital) dipole moment $\mu_l$ . The direction of this dipole moment is given by the right-hand rule (see diagram below). Quantum mechanically, this corresponds to the magnetic moment associated with orbital angular momentum.

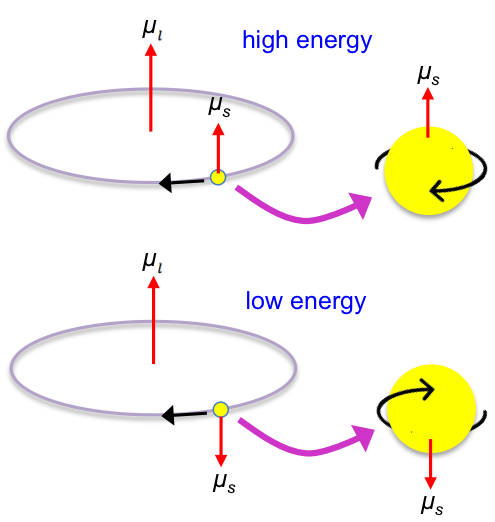
In addition to this orbital magnetic moment, the electron possesses an intrinsic magnetic dipole moment due to its spin—a quantum property not arising from literal rotation. Nevertheless, the magnetic (spin) dipole moment $\mu_s$ behaves similarly to that of a tiny current loop.

Since the spin and orbital magnetic dipole moments are vector quantities, they interact through a mechanism known as spin-orbit coupling. When the allowed spin states correspond to the spin and orbital angular momenta being either aligned (parallel) or opposed (anti-parallel), the coupling results in two quantum states with different energies.

Question

What is a magnetic dipole moment?

Answer

According to classical electromagnetic theory, a moving charge generates a magnetic field, which implies the presence of north and south magnetic poles called a magnetic dipole. The magnetic dipole moment is a measure of the strength and orientation of a magnetic dipole, i.e. a vector.

This is the reason why an electron, when excited to the n = 2 shell of the hydrogen atom, has one of two possible states (energy levels), namely ²P_3/2 and ²P_1/2. When the electron relaxes back to the n = 1 shell, one of two emission lines is observed, depending on whether the electron was initially promoted to the upper or lower state. The concept of electron spin and quantised spin orientations are validated by the Stern-Gerlach experiment, where a beam of silver atoms is directed through a magnetic field gradient.

In solving the Schrodinger equation for the hydrogen atom, the quantum number $l$ is attributed to the angular momentum of the electron as it orbits the nucleus. Since a particle possesses angular momentum, whether orbiting or spinning, a spinning electron has spin angular momentum. Furthermore, we know from the solution of Schrodinger’s equation that each value of $l$ (a vector) is associated with orientations of the magnetic number $m_l$ , where $m_l=-l,-l+1...0...l-1,l$ . With that, Pauli proposed a fourth quantum number $m_s$ , the spin magnetic number, to fully describe the quantum state of a system. Like $m_l$ , $m_s=-s,-s+1...0...s-1,s$ . The value of $s$ (another vector) was later experimentally determined to be $\frac{1}{2}$ . Therefore, $s$ has two possible orientations of $m_s=-\frac{1}{2}\; or\; +\frac{1}{2}$ .

Question

Shouldn’t the n = 1 shell split into two energy levels too?

Answer

The explanation above provides a qualitative picture of spin-orbit coupling. Mathematically, the spin-orbit interaction energy is computed using the formula:

$E=\frac{1}{2}hcA[j(j+1)-l(l+1)-s(s+1)]$

where h, c and A are constants, and j is a non-negative number known as the total angular momentum quantum number (i.e., the vector sum of $l$ and $s$ ), with the possible values of $j=l+s,l+s-1,l+s-2,\cdots,\vert l-s\vert$ .

According to the solution of the Schrodinger equation, when $n=1$ , we have $l=0$ , which makes j = s. Substituting these values in the above equation yields a single value of E = 0. This means that there is no effect of spin-orbit coupling on the quantum state of n = 1. Using the same logic, we find that the quantum state “ $n=2,l=1$ ” gives two values of E, $\frac{1}{2}hcA$ and $-\frac{1}{2}hcA$ , resulting in the states ²P_3/2 and ²P_1/2.