An s-orbital is a spherical region of space around the nucleus where an electron with zero orbital angular momentum is most likely to be found. The letter ”s” is of spectroscopic origin, standing for ‘sharp’.
One-electron s-orbital wavefunctions can be expressed using the total wavefunction of a hydrogenic atom:
where
, the radial wavefunction, is the radial component of
.
, the spherical harmonics, is the angular component of
.
are the associated Laguerre polynomials.
are the associated Legendre polynomials.
is the normalisation constant of the radial wavefunction.
is the normalisation constant of the spherical harmonics.
is the principal quantum number, where
is the orbital angular momentum quantum number (also known as azimuthal quantum number), where
and
.
is the magnetic quantum number, where
.
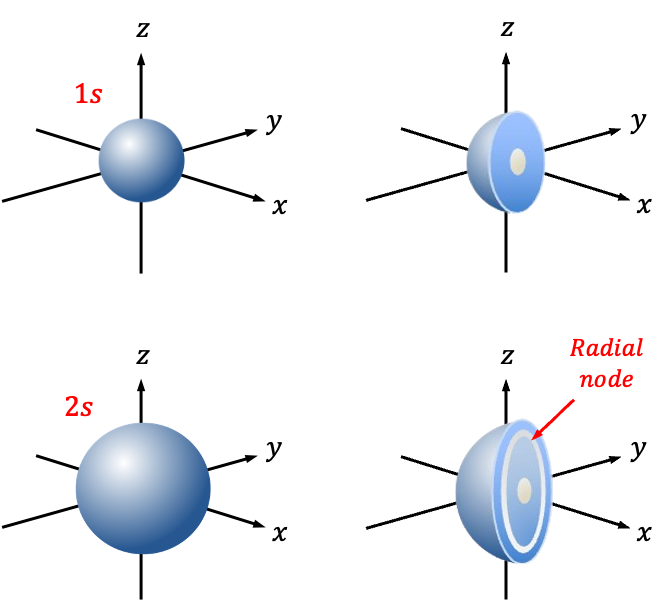
The principal quantum number, , is also called a shell. Since the first shell is characterised by
, the one-electron s-orbital wavefunction in the first shell, known as the 1s orbital, is defined by the set of quantum numbers
. Substituting these values into the explicit formula for
yields:
Similarly, the one-electron s-orbital wavefunction in the second shell, known as the 2s orbital, is defined by the set of quantum numbers and has the formula:
Since for all s-orbitals, their wavefunctions are independent of
and
. This implies that the values of an s-orbital wavefunction are the same in all directions in 3D space for a given
. In other words, s-orbital wavefunctions are spherically symmetrical.
Finally, the 1s orbital and 2s orbital have 0 radial nodes and 1 radial node, respectively (see above diagram).