The vector model of angular momentum is a diagrammatic representation of the implications of the commutation relation of with any one of the 3 component angular momentum operators. In a previous article, we showed that it is possible to simultaneously specify eigenvalues of
and
because the 2 operators commute. Diagram I depicts the eigenvalues of
(i.e. the square root of eigenvalues of
) and
.
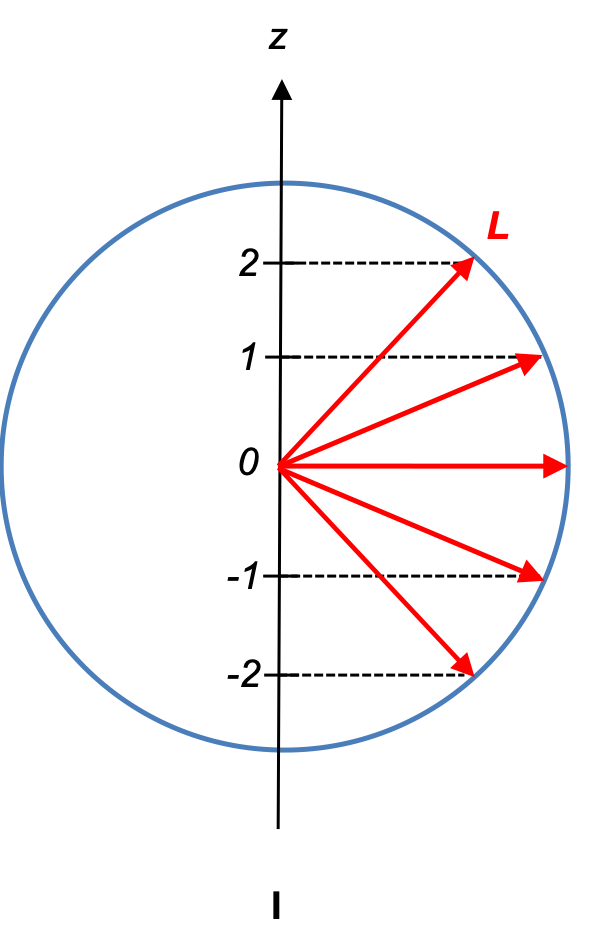
where axes are in units;
is the angular momentum vector with magnitude
, and has a
-component of magnitude
.
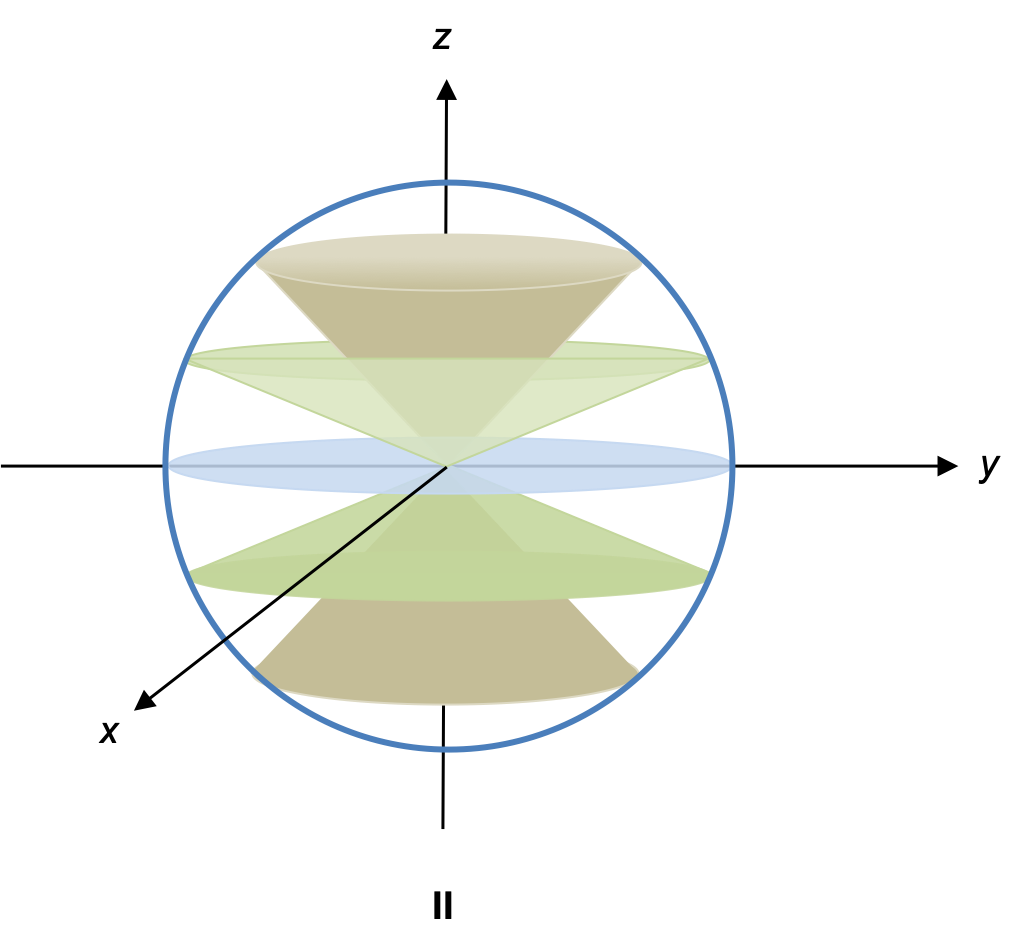
Since any one of the component angular momenta does not commute with any of the other two, we cannot simultaneously specify more than one component of angular momentum (other than the trivial case of ). The angular momentum vector therefore lies on the cones in diagram II at any azimuthal angle.

Question
Can lie on the
-axis?
Answer
No. If lies on the
-axis,
is some non-zero integer while
. This means we have specified all 3 angular momentum components, which is impossible.
