Larmor precession is the change in orientation of the axis of the magnetic moment of a particle with respect to the axis of an external magnetic field. Consider an electron at rest with intrinsic spin of
in a
-directional uniform magnetic field
. The magnetic field interacts with the electron’s magnetic moment and generates a torque
(see diagram below).
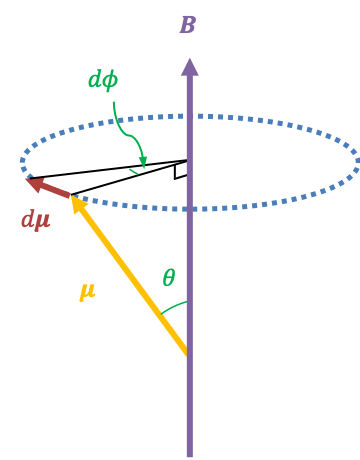
If is the spin magnetic moment of an electron, eq61 becomes
, where
is the gyromagnetic ratio of the electron. Taking the derivative on both sides of this equation with respect to
,
From eq64 and eq71, we have , whose spin analogue is
. So,
With reference to the above diagram, the change in arc length with respect to is
. Hence,
where is the period,
is the mass of an electron and
is the Larmor frequency, which is defined as a positive value.
Note that the Larmor frequency is sometimes defined as , which is then
.