The electron, as shown in the Stern-Gerlach experiment, has a form of angular momentum called spin angular momentum, in addition to its orbital angular momentum.
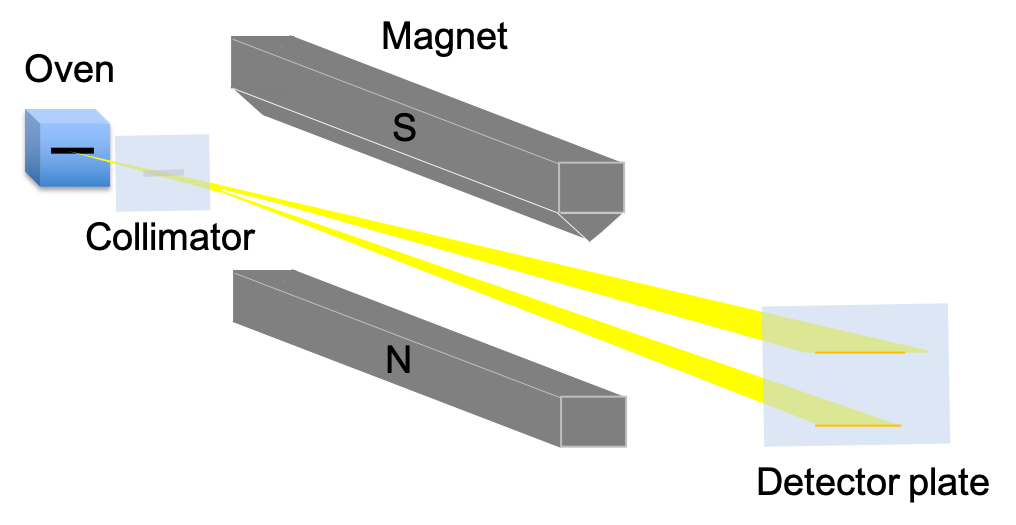
The spin angular momentum of an electron is referred to as an intrinsic angular momentum because it is similar in certain ways to classical spin (e.g. it is associated with a magnetic dipole moment) but is purely a quantum mechanical effect. It is erroneous to view the electron as spinning about its own axis.
The theory of quantum mechanics postulates that spin angular momentum operators are linear and Hermitian, and obey the same commutation relations as described by eq99, eq100 and eq101, i.e.:
Therefore, the corresponding equations of eq132, eq133 and eq148 are:
respectively, where is the spin angular momentum quantum number;
is the spin magnetic quantum number;
.
For an electron, has been determined experimentally not to have a range of values but to be specifically equal to
. We say that electrons have spin
. Similarly, both protons and neutrons have spin
.