Symmetry and degeneracy are related as a result of the non-relativistic Hamiltonian being invariant under symmetry operations.
Consider the stationary state of a quantum mechanical system that is described by a set of linearly independent wavefunctions , which satisfies the time-independent Schrodinger equation
. Subjecting both sides of the equation to the symmetry operation
, where
are elements of a group
, we have
. Using eq53 and noting that
is a scalar, we obtain
which implies that is an eigenfunction of
, i.e.
.
We say that the set of symmetry operations form the group of the Hamiltonian. If is
-fold degenerate, any linear combination of the subset of wavefunctions
associated with the degenerate eigenvalue will be a solution of eq54. We can then write:
According to the closure property of ,
So,
Since is a linear operator,
Subtracting eq59 from eq57, we have . If the wavefunctions are linearly independent, all coefficients of
must be zero, i.e.
With reference to eq55 through eq57, and
range from
to
. Thus, eq60 implies that
and
are entries of the square matrices
and
respectively, i.e.
Comparing eq61 with eq58, the matrices and
multiply the same way as the symmetry operations
and
and therefore form a representation
of
. Such a representation has a dimension equal to
and may be reducible or irreducible. However, the following analysis shows that it is irreducible, assuming that there is no accidental degeneracy, which happens when two eigenvalues are the same even though their corresponding eigenfunctions transform differently under the symmetry operations of
.

Question
What is an example of accidental degeneracy?
Answer
The hydrogenic wavefunctions and
, which describe the
-orbital and
-orbitals respectively, obviously have different symmetry and may transform according to different irreducible representations, e.g. the
-orbital transforms according to the totally symmetric irreducible representation, while the
-orbitals may not. Therefore, they may have different energies. However,
and
are degenerate wavefunctions for a particular value of
. In fact, the number of degenerate energy levels of the hydrogen atom is
instead of
, which is expected from a non-relativistic Hamiltonian with a central potential. This implies that spin-orbit coupling is not considered when deriving the hydrogenic wavefunctions. The degeneracy is lifted once spin-orbit coupling is included.
To show that is irreducible, we express eq55 as
where .
If is reducible, then it may be in block-diagonal form. For example, if
,
Substituting eq61b in eq61a, and
are linear combinations of the subset with elements
and
, while
and
are linear combinations of the subset with elements
and
. If so, the eigenvalues corresponding to the different subsets could be different (e.g. when one subset is one-dimensional and the other is two-dimensional), which would contradict our original assumption that
is
-fold degenerate.
If is not initially in block-diagonal form, it can be converted into a block-diagonal matrix
via a similarity transformation, where
. We can then rewrite eq61a as
where is the basis for the transformed representation.
Since is in block-diagonal form, we arrive at the same conclusion as before. Therefore, assuming that there is no accidental degeneracy, a representation that is generated by a set of orthogonal degenerate wavefunctions is irreducible and we called the set of wavefunctions
, basis wavefunctions of
.

Question
1) Why is the number of basis functions needed to generate equal to the dimension of
?
2) Can any set of functions, other than eigenfunctions of the Hamiltonian, be a set of basis functions for a representation of ?
3) Show that if is a basis of a representation
of a group, then any linear combination of
is a basis of a representation
that is equivalent to
.
Answer
1) Each in
of eq55 creates a column of matrix entries
(see Q&A below for an illustration). So, the
matrix
is generated by
number of
. The same logic applies to matrices
and
. This implies that the number of linearly independent basis functions of a representation corresponds to the dimension of the representation. This set of linearly independent basis functions can be made orthogonal to one another using the Gram-Schmidt process. Therefore, the number of orthogonal basis functions of a representation corresponds to the dimension of the representation.
2) By inspecting eq55 through eq61, any set of linearly independent functions , not necessary eigenfunctions of the Hamiltonian, is a set of basis functions for a representation of
if
is transformed by a symmetry operation into a linear combination of
. The converse is obviously also true, i.e. if
is a set of basis functions for a representation of
, then
. In this case, there is no requirement that the functions are degenerate and hence the representation generated can be either reducible or irreducible.
3) Since matrix multiplication is distributive,
Let’s rewrite eq55 as . Substituting this expression in the above equation and rearranging, gives
where .
Using eq61d and repeating the steps from eq55 through eq61, is also basis of a representation
of the group.
To Show that is equivalent to
, let
, which can be written as the following matrix equation:
where .
Using eq55 with in place of
, we have
, whose matrix equation is
where .
Multiplying eq61e by on the right, we have
, which when substituted in eq61f gives
The matrix equation of eq55 with in place of
is
Comparing eq61g with eq61h, is related to
by a similarity transformation. This implies that
is equivalent to
.
If is non-degenerate, the only eigenfunctions satisfying eq54 are
, where
is a constant. Therefore,
. Normalising
, we get
, which means that
. Consequently, the wavefunctions
associated with non-degenerate eigenvalues transform according to one-dimensional irreducible representations with characters of +1 or -1.

Question
If , show how eq55 is related to the matrix representation
.
Answer
The two degenerate wavefunctions are and
. We have
We can conclude from the above analysis that irreducible representations with dimension of one are called non-degenerate representations, while those with dimensions of more than one are known as degenerate representations.

Question
With regard to the symmetry operation of the
point group, show that
and
transform together according to the two-dimensional irreducible representation
.
Answer
With respect to the green line in the below diagram depicting the spherical coordinate system, and
are invariant to the
symmetry operation of the
point group.
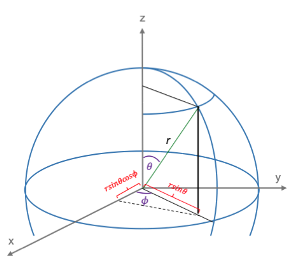
The and
wavefunctions in spherical coordinates are
and
.
In other words, the symmetry operation transforms
into a linear combination of
and
(c.f. eq55). Similarly,
Therefore, and
transform together according to the two-dimensional irreducible representation
, with the coefficients of the basis functions
and
in eq62 and eq63 being the entries of the matrix
.
Repeating the same procedure shown in the Q&A above for the rest of the symmetry operations of the point group, we have
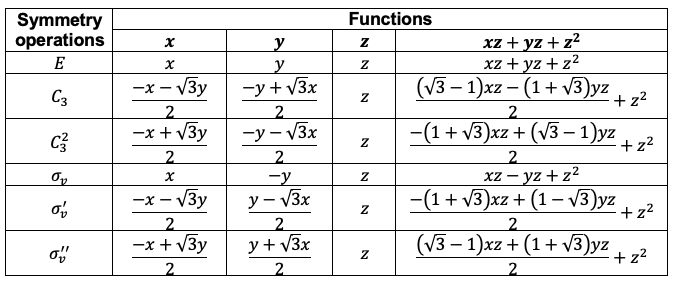
The transformation of the function is determined by summing the separate transformations of the
-orbitals
and
.