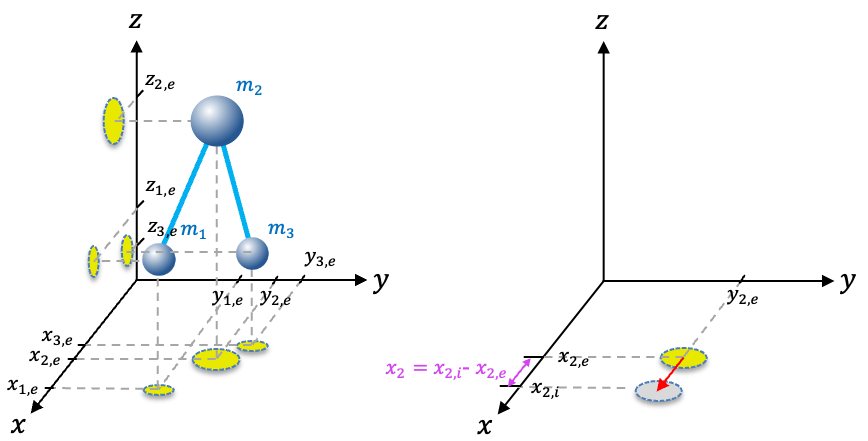
The vibration of polyatomic molecules involves stretching, bending and torsional motions.
The classical kinetic energy of a vibrating
-nuclei molecule is
where ,
and
are the displacements of the
-th nucleus from its equilibrium position of
(see diagram below).
Eq85 can be simplified by changing the Cartesian displacement coordinates to mass-weighted displacement coordinates
, where
which gives
where and
is a column vector with elements
.
The potential energy of a vibrating
-nuclei molecule is also a function of
and hence a function of
. We can approximate the multivariable function
by expanding it in a Maclaurin series around the equilibrium positions:
which can be abbreviated to
When the nuclei are at their equilibrium positions, the slope of is zero, i.e.
. For small vibrations, where
is close to
, we ignore all the higher power terms, giving
or in matrix notation
where is the column vector with elements
and
is a
matrix, called the Hessian matrix, with elements
.

Question
Show that .
Answer
We want to derive an eigenvalue equation that resembles the harmonic oscillator equation so that we can easily solve for the vibrational energies of a polyatomic molecule. However, the Hamiltonian formed by combining eq86 and eq87 doesn’t resemble the Hamiltonian of a harmonic oscillator. Therefore, we need to further simply eq86 and eq87 with a change of variables.
With regard to eq88, the potential energy of a system is a real-valued physical property. This implies that must consists of real-valued entries
. Since
, the matrix
is both real and symmetric.

Question
i) Prove that eigenvectors of a real and symmetric matrix with distinct eigenvalues are orthogonal.
ii) What if some of the eigenvalues are degenerate?
Answer
i) Let and
, where
. Multiply the first eigenvalue equation by
, we have
where the 2nd equality uses the identity mentioned in this article, while the 3rd equality employs the property of a symmetrc matrix.
Since , we have
, i.e.
is orthogonal to
.
ii) When some eigenvalues are degenerate, the corresponding eigenvectors belong to the same eigenspace. Since we can always select a set of linearly independent eigenvectors that span the eigenspace, these eigenvectors can be orthogonalised using the Gram-Schmidt process without changing the eigenvalue. So, for a real symmetric matrix, we can always find a basis of eigenvectors that are orthogonal to each other, regardless of whether the eigenvalues are distinct or degenerate.
Let the orthogonal eigenvectors of
be the columns of the matrix
, where
. As shown in this article, we can express the eigenvalue problem
as
where is the diagonal eigenvalue matrix with diagonal entries
.
Computing the secular equation allows us to find
, and solving the simultaneous equations of
, which is equivalent to
(where
, enables us to find
.
Consider the following linear combinations of mass-weighted displacement coordinates
where is the column vector with elements
.
Since are the components of the
-th orthogonal eigenvector of
and each basis
describes the displacement of a nucleus,
, known as the normal coordinates, is a set of orthogonal vectors that expresses
independent motions (called degrees of freedom) of the molecule as a whole.
Substituting in eq88
Since , we have
or
and eq86 becomes
Combining eq90 and eq91, the classical total energy of the system is , where we have set
. This is because we are usually interested in computing transition energies and the eigenvalue corresponding to
is subtracted out when we calculate vibrational transition energies for a given electronic state. The Hamiltonian is derived by replacing the classical observables by quantum-mechanical operators:

Question
Show that the classical kinetic energy term can be replaced by the quantum-mechanical operator
.
Answer
From eq89, . Substituting the momentum operator
in
, we have
. Using the single-variable chain rule
, we have
, which when substituted in
gives
. We can find similar expressions for
. So,
. Since
is a function of
, and
is a function of
, the multi-variable chain rule gives
. Relabelling
as
, we have
and therefore,
, which when substituted in
gives
. Substituting this last expression of
in
gives
.
The kinetic energy term in eq92 involves a change in , which is a function of
and hence a function of the displacement coordinates
,
and
, which are relative to the equilibrium positions of the nuclei. In other words,
is a function of the displacements of all the nuclei from their respective equilibrium positions. For the molecule as a whole, all the equilibrium positions of the nuclei can be taken as the center of mass of the molecule. Since translational and rotational motions of the molecule involve no displacement relative to the molecule’s centre of mass,
for such motions. Furthermore, translational and rotational motions are purely kinetic with no potential energy component. Therefore, we can rewrite eq92 as:
where and
for a non-linear molecule and a linear molecule respectively.
Each is called a normal mode and corresponds to a unique vibrational motion of the molecule. The Schrodinger equation is
where the separation of variables technique allows us to approximate the total vibrational wavefunction as and hence,
.
It follows that each describes a normal mode of the molecule. Comparing with eq4a, eq93 is the Schrodinger equation for a harmonic oscillator of unit mass and force constant
. This implies that (see eq46)
where is the normalisation constant for the Hermite polynomials
.
Therefore, eq93 can be solved by computing individual Schrodinger equations. With reference to eq21, each solution gives
where is the vibrational quantum number of the
-th normal mode of the molecule.
The total vibrational energy is
The vibrational state of a polyatomic molecule is characterised by
quantum numbers. For example the vibrational ground state of
, where
, is
. The ground state vibrational wavefunction of any polyatomic molecule is
Eq97 is a Gaussian function that is symmetrical in . The implication of this in group theory is that the ground state vibrational wavefunction of any polyatomic molecule is totally symmetric under all symmetry operations of the point group that the molecule belongs to. In fact, group theory provides an easy way to determine the vibrational modes of a molecule and to analyse the possible transitions between different vibrational states.