Degeneracy in hydrogenic atoms

Degeneracy in hydrogenic atoms refers to the number of possible states corresponding to a given energy value of a hydrogenic wavefunction.

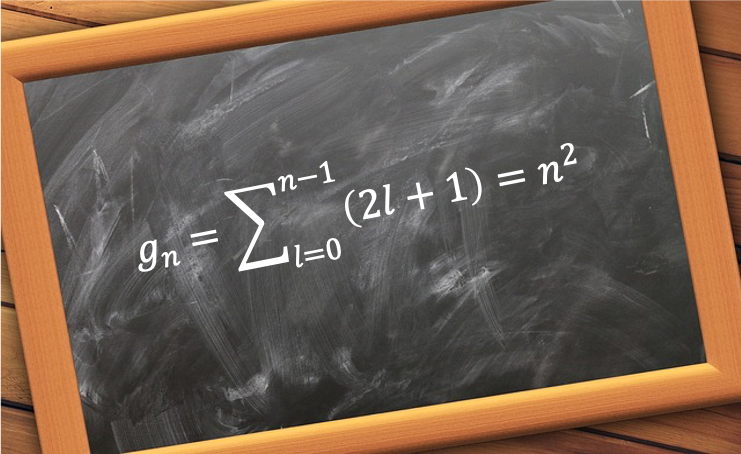
The total wavefunction of a hydrogenic atom is characterised by three quantum numbers: $n$ , $l$ and $m_l$ . This implies that the state of the atom is defined by the set of quantum numbers $\{n,l,m_l\}$ . However, in a hydrogenic atom, the nucleus acts effectively as a point charge, and the electrostatic potential energy is spherically symmetric. This spherical symmetry means that the energy of the electron depends only on its distance from the nucleus. In other words, the energy of the electron is the eigenvalue associated with the radial component of the total wavefunction. As shown in eq462b, this eigenvalue is governed solely by the principal quantum number $n$ . Consequently, all the possible energy states defined by $\{n,l,m_l\}$ for a given $n$ must have the same energy and are therefore degenerate.

Since $l=0,1,2,\cdots$ (see this article for explanation) and $l\leq n-1$ (see eq462a), the possible values of the orbital angular momentum quantum number $l$ range from 0 to $n-1$ for a given $n$ . Furthermore, for each value of $l$ , the magnetic quantum number $m_l$ can take on $2l+1$ values (see this article for explanation). Therefore, the degeneracy $g_n$ for a given $n$ is the sum of all the possible values of $m_l$ for each $l$ from 0 to $n-1$ :