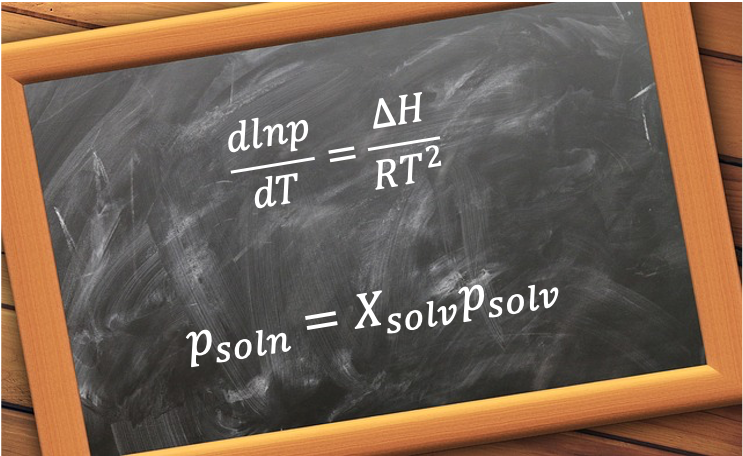A permutation of a set is an ordered arrangement of its elements.
Distinct elements
Consider the task of filling  buckets, each with a ball chosen from a pool of
buckets, each with a ball chosen from a pool of  distinct numbered balls. There are
distinct numbered balls. There are  possible choices for the first bucket. Once the first ball is used, only
possible choices for the first bucket. Once the first ball is used, only 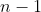 choices remain for the second bucket, then
choices remain for the second bucket, then 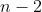 choices for the third bucket, and so on. This continues until the last bucket, for which only 1 ball remains.
choices for the third bucket, and so on. This continues until the last bucket, for which only 1 ball remains.
If you have 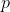 ways to do a first task, and for each of those,
ways to do a first task, and for each of those, 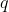 ways to do a second task, then the total number of ways to perform both tasks is
ways to do a second task, then the total number of ways to perform both tasks is  . This principle extends to any number of sequential tasks. Therefore, the total number of distinct arrangements (permutations) of the
. This principle extends to any number of sequential tasks. Therefore, the total number of distinct arrangements (permutations) of the  balls in
balls in  buckets, denoted by
buckets, denoted by ) or
or  , is the product of the number of choices for each task:
, is the product of the number of choices for each task:
=n(n-1)(n-2)\cdots(2)(1)=n!)
Now, suppose there are  distinct balls but only
distinct balls but only  buckets, where
buckets, where  . Again, there are
. Again, there are  choices for the first bucket,
choices for the first bucket, 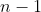 for the second, and so on until the
for the second, and so on until the  -th bucket. Since we can also express the number of choices for the second bucket as
-th bucket. Since we can also express the number of choices for the second bucket as  , we have
, we have  ways of filling the
ways of filling the  -th bucket. Hence,
-th bucket. Hence,
=n(n-1)(n-2)\cdots(n-r+1)\;\;\;\;\;\;\;\;306)
Multiplying RHS of eq306 by !}{(n-r)!}) gives
gives
=n(n-1)(n-2)\cdots(n-r+1)\frac{(n-r)!}{(n-r)!}=\frac{n!}{(n-r)!}\;\;\;\;\;\;\;\;307)
Eq307 gives the general formula for calculating permutations — the number of ways to arrange  objects selected from a set of
objects selected from a set of  distinct objects.
distinct objects.

Question
In a lottery draw for a four-digit winning number, each digit can be any number from zero to nine. How many permutations are possible?
Answer
Total permutations = 10 x 10 x 10 x 10 = 104. In general, the number of permutations for forming a sequence of  positions, where each position can be filled with
positions, where each position can be filled with  possible choices is
possible choices is  .
.
Repeating elements (multinomial permutation)
How many distinct permutations are there of the letters in the word “MISSISSIPPI”? If all letters were distinct, the number of permutations would be 11! = 39,916,800. However, some letters are repeated in the word: 4 I’s, 4 S’s, 2 P’s and 1 M. To understand why we need to adjust for repeated letters, let’s consider the I’s. Suppose we label the four I’s as I1, I2, I3 and I4, treating them as distinct. In any arrangement, these four labelled I’s can be rearranged among themselves in 4! = 24 ways. For example, we could have:
M I1 S S I2 S S I3 P P I4
M I1 S S I2 S S I4 P P I3
M I2 S S I1 S S I3 P P I4
…and so on.
But since these I’s are actually indistinguishable, all 24 of those arrangements represent the same permutation of the word. So, we’ve overcounted each unique arrangement by a factor of 4!. Similarly, the 4 S’s and 2 P’s can be rearranged in 4! ways and 2! ways respectively. Each of these reorderings also causes overcounting, resulting in a total overcounting factor of 4! x 4! x 2!. Therefore, to find the number of distinct permutations of the letters in “MISSISSIPPI”, we divide the total number of arrangements by the total repeated counts:  .
.
In general, if you have a set of  objects, where
objects, where 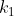 are identical to each other,
are identical to each other, 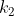 are identical to each other but different from the first group, and so on until
are identical to each other but different from the first group, and so on until 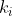 , each representing a distinct group of identical items, then the number of distinct permutations is:
, each representing a distinct group of identical items, then the number of distinct permutations is:

where  and
and  is also known as the multinomial coefficient.
is also known as the multinomial coefficient.
Eq308 is used to derive the Boltzmann distribution and Raoult’s law.
A combination is a selection of items where the order does not matter. For example, AB and BA are two different permutations of the set {A,B}, but they represent the same combination. To calculate the number of combinations, we start by counting the permutations (where order does matter), and then correct for overcounting by dividing out the number of ways the selected items can be rearranged.
Suppose we are selecting  objects from a set of
objects from a set of  distinct objects. The number of permutations is given by eq307:
distinct objects. The number of permutations is given by eq307: !}) . However,
. However,  items can be arranged in
items can be arranged in  ways, all of which count as the same combination when order doesn’t matter. There, the number of combinations, denoted by
ways, all of which count as the same combination when order doesn’t matter. There, the number of combinations, denoted by ) or
or  or
or ) , is
, is
=\frac{n!}{r!(n-r)!}\;\;\;\;\;\;\;\;309)
Interesting, the number of combinations is also the binomial coefficient.

Question
Show that a mutlinomial permutation can be expressed as a product of combinations.
Answer
Suppose we want to partition a set of  distinct items into
distinct items into 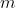 groups of specified sizes
groups of specified sizes 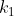 ,
, 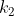 , …,
, …, 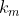 , where
, where  . The number of ways to select
. The number of ways to select 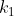 items for the first group is
items for the first group is
=\frac{n!}{k_1!(n-k_1)!})
The number of ways to select the remaining  items for the second group is
items for the second group is
=\frac{(n-k_1)!}{k_2!(n-k_1-k_2)!})
The number of ways to select the remaining  items for the third group is
items for the third group is
=\frac{(n-k_1-k_2)!}{k_3!(n-k_1-k_2-k_3)!})
and so on until the remaining the number of ways to select the remaining 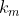 items for the last group is
items for the last group is

Therefore, the total number of ways to perform all the sequential tasks is
!}\frac{(n-k_1)!}{k_2!(n-k_1-k_2)!}\frac{(n-k_1-k_2)!}{k_3!(n-k_1-k_2-k_3)!}\cdots\frac{k_m!}{k_m!0!})
which simplifies to the RHS of eq308 after all the cancellations.
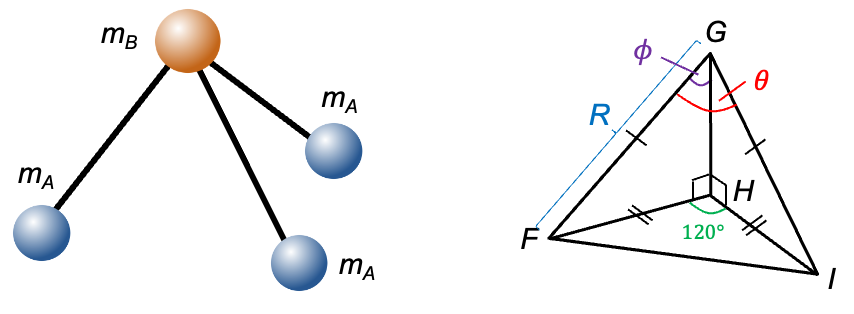
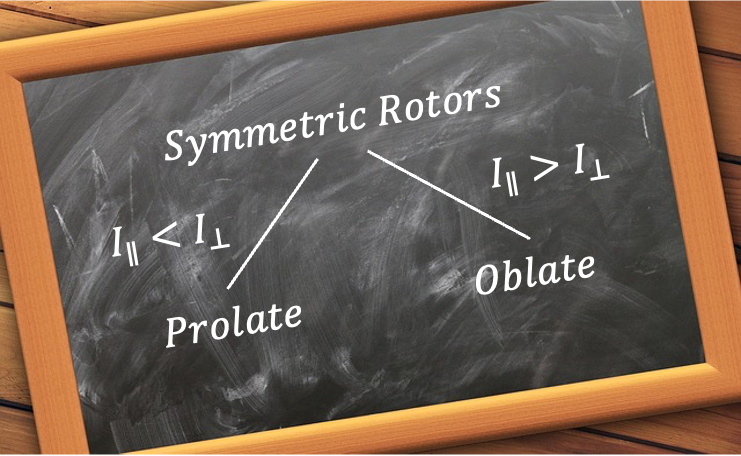
symmetry (e.g. CHCl3) are characterised by a unique moment of inertia
around the principal axis and two equal moments of inertia
perpendicular to the principal axis, where
. They are derived using simple geometric considerations.
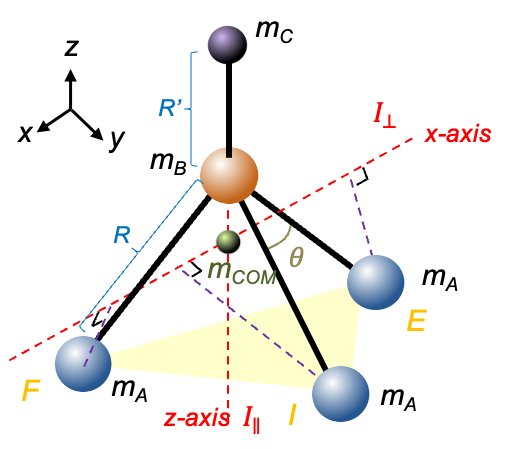
axis (
-axis) of the molecule has the same symmetry as a trigonal pyramidal molecule, the moment of inertia for symmetric rotors like CHCl3 along the
-axis is given by eq22:
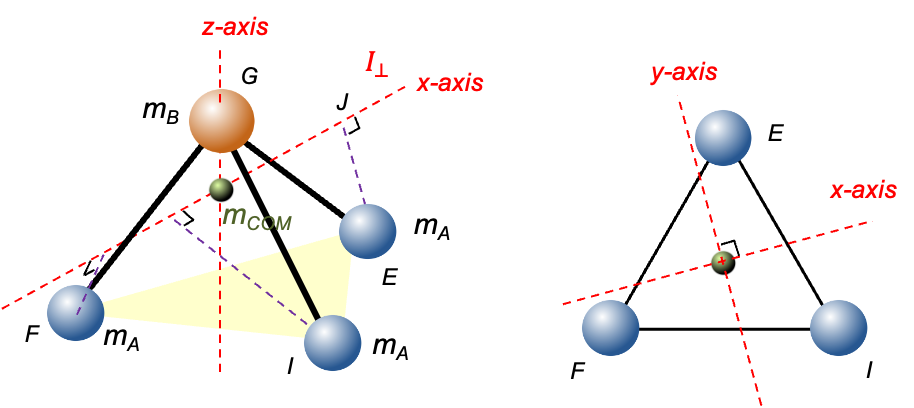
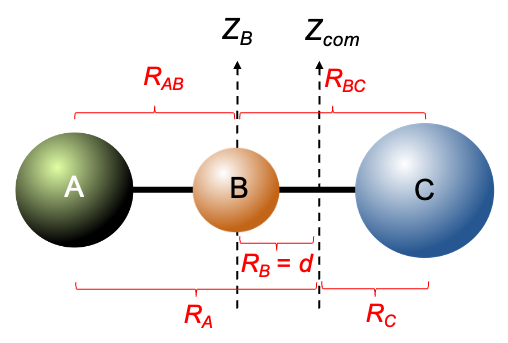
, place the origin at the centre of mass of the molecule. The
-coordinates of atom C, atom B and each of the A atoms are
,
and
respectively. Then, the centre of mass of the molecule satisfies
or
and
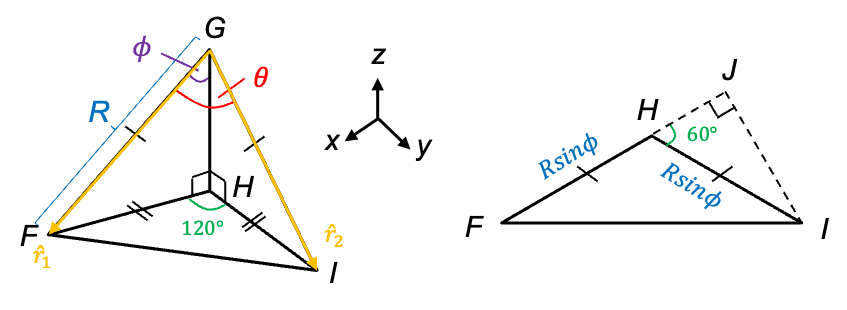
coordinates of the three A atoms defined in the previous article, the positions of the atoms are:
, the moment of inertia of the molecule about the
-axis is
. Substituting the data from the above table and eq23 into this equation gives:
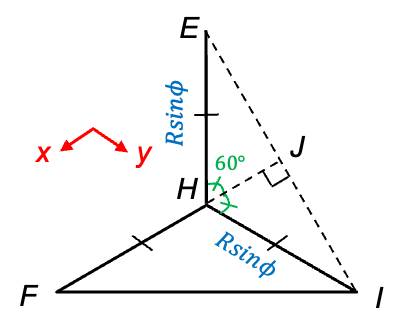
-axis
, and then substituting eq23 into the resultant equation, yields the same expression as eq33. Therefore, eq22 and eq33 represent two distinct moments of inertia of a tetrahedral prolate rotor with
symmetry.

symmetry. You can convince yourself by deriving the expression using the geometry of CH3Cl.