Vanishing integrals

A vanishing integral is a continuous sum of a function that evaluates to zero. Group theory allows us to identify a vanishing integral as a result of the symmetry of the system.

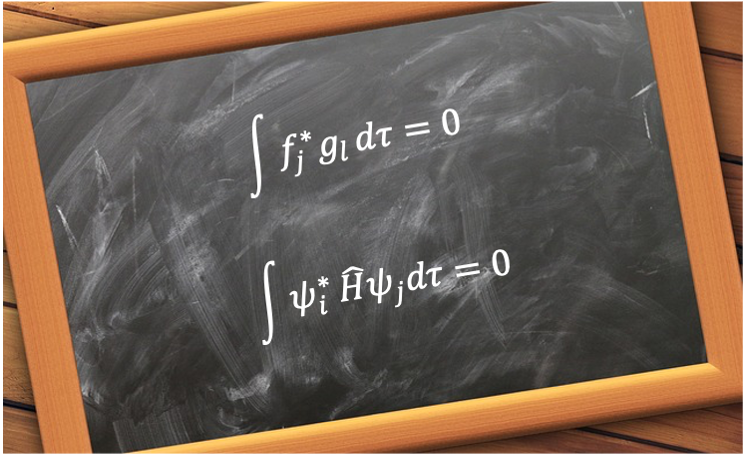
Consider a set of basis functions $\{ j_q\}$ that transforms according to a representation $\Gamma_q$ of a point group $G$ . The integral of an element of the function $\int j_qd\tau$ is a scalar, which is invariant to any symmetry operation $R_{\alpha}$ of the coordinate system, i.e.

$\int j_qd\tau=R_{\alpha}\int j_qd\tau=\int R_{\alpha}j_qd\tau\;\;\;\;\;\;\;\;82$

Since there are $\vert G\vert$ number of symmetry operations of $G$ , we can write $\vert G\vert$ equations of eq82 and sum them to give

$\vert G\vert\int j_qd\tau=\int\sum_{\alpha=1}^{\vert G\vert}R_{\alpha}j_qd\tau\;\;\;\;\;\;\;\;83$

Let $j_q=f_j^*g_l$ , where $f_j$ and $g_l$ belong to the sets of linearly independent functions $\{ f_1,f_2,\cdots,f_m\}$ and $\{ g_1,g_2,\cdots,g_n\}$ respectively, and where $f_m$ and $g_n$ are bases for the irreducible representations $\Gamma_f$ and $\Gamma_g$ respectively of $G$ . Substituting $j_q=f_j^*g_l$ and eq77i in eq83,

$\int f_j^* g_ld\tau=\frac{1}{\vert G\vert}\sum_{i=1}^m\sum_{k=1}^n\sum_{\alpha=1}^{\vert G\vert}a_{ij}^*b_{kl}\int f_i^*g_kd\tau\;\;\;\;\;\;\;\;84$

Rewrite eq20 as $\sum_{\alpha}^{\vert G\vert}a_{ij}^*b_{kl}=0$ and substitute it in eq84 to give

$\int f_j^* g_ld\tau=0\;\;\;\;\;\;\;\;85$

We conclude that:

Rule 1

If $\boldsymbol{\mathit{f_j}}$ and $\boldsymbol{\mathit{g_l}}$ transform according to two different non-equivalent irreducible representations $\boldsymbol{\mathit{\Gamma_f}}$ and $\boldsymbol{\mathit{\Gamma_g}}$ respectively, the integral of their product over all space is necessarily zero

This implies that basis functions belonging to different non-equivalent irreducible representations are orthogonal. With respect to eq76 and eq77i, if $f_j$ transforms according to the totally symmetric representation of $G$ and $g_l$ transforms according to a different irreducible representation $\Gamma_g$ of $G$ , then $j_q$ must transform according to $\Gamma_g$ , which is obviously not the total symmetric representation of $G$ . Therefore,

Rule 2

If a function transforms according to an irreducible representation that is not the totally symmetric representation of a group, its integral over all space is necessarily zero

Next, we look at the quantum-mechanical integral $\int f_a^*f_bf_cd\tau$ , where $f_a^*$ and $f_c$ are wavefunctions and $f_b$ is a quantum-mechanical operator, which is also a function.

Question

Why is an operator a function?

Answer

A function $f:A\rightarrow B$ is a mapping of each element of the set $A$ in one vector space of functions $V$ to one element of the set $B$ in another vector space of functions $W$ , which may be the same space as $V$ . Similarly, an operator maps each element (e.g. a wavefunction) of a vector space of functions $M$ to another element in another vector space of functions $N$ , which may be the same space as $M$ .

Due to rule 1, $\int f_a^*f_bf_cd\tau$ is necessarily zero if $f_a^*$ and $f_bf_c$ transform according to two different non-equivalent irreducible representations. Let’s consider the integral $\int \psi_i^*\hat{H}\psi_jd\tau$ , where $\psi_i^*$ , $\hat{H}$ and $\psi_j$ transform according to the irreducible representations $\Gamma_1$ , $\Gamma_2$ and $\Gamma_3$ respectively of a group $G$ . Since the non-relativistic Hamiltonian $\hat{H}$ is invariant under any symmetry operation, it transforms according to the totally symmetric irreducible representation of $G$ . With reference to eq76 and eq77i, $\hat{H}\psi_j$ consequently transforms according to $\Gamma_3$ . Therefore, $\int \psi_i^*\hat{H}\psi_jd\tau=0$ if $\Gamma_1\neq\Gamma_3$ .

Question

Do the integrals $\int \psi_{d_{xy}}^*\hat{H}\psi_{d_{yz}}d\tau$ and $\int \psi_{d_{xy}}^*\hat{x}\psi_{d_{yz}}d\tau$ vanish in a $C_{2v}$ molecule?

Answer

$\hat{H}$ is totally symmetric, while $\psi_{d_{xy}}^*$ and $\psi_{d_{yz}}$ transform according to two different non-equivalent irreducible representations $A_2$ and $B_2$ respectively. Therefore, $\int \psi_{d_{xy}}^*\hat{H}\psi_{d_{yz}}d\tau=0$ . Using eq76, $\hat{x}\psi_{d_{yz}}$ transforms according to $A_2$ . Hence, $\int \psi_{d_{xy}}^*\hat{x}\psi_{d_{yz}}d\tau$ is not necessarily zero.